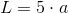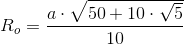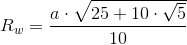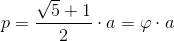Pięciokąt foremny i pentagram

Stronę tą wyświetlono już: 8323 razy

Podstawowe cechy szczególne

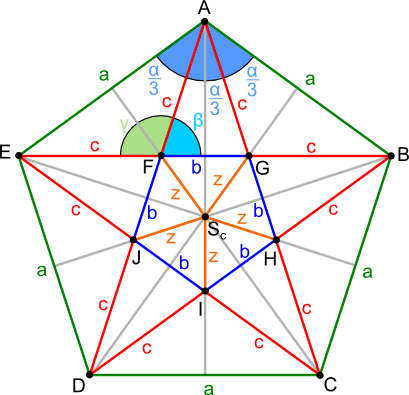
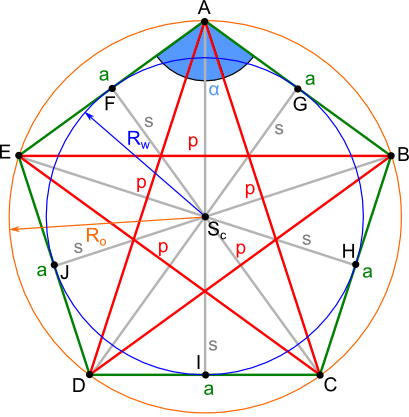
Każdy kąt wewnętrzny pięciokąta foremnego jest równy 108°, zaś jego środek ciężkości, środek okręgu opisanego, środek okręgu wpisanego, punkt przecięcia się symetralnych boków oraz punkt przecięcia się symetralnych kątów wewnętrznych pięciokąta foremnego znajdują się w jednym i tym samym punkcie S_c. Pięciokąt foremny, jest wielokątem foremnym o największej liczbie boków, którego wszystkie przekątne p mają takie same długości. Wszystkie przekątne łączą się z sobą tworząc figurę geometryczną zwaną pentagramem. Każda symetralna s boku pięciokąta foremnego jest równocześnie symetralną jego kąta wewnętrznego.

Stosunek długości przekątnej p do długości boku a pięciokąta foremnego jest dany następującą zależnością:

[1]

Zapis wyrażenia w formacie TeX-a:

\frac{p}{a}=\varphi

gdzie φ jest to liczba złota, której wartość wynosi około 1,6180339887...

Trójkąty równoramienne o ramionach długości przekątnej p i buku długości a oraz o długości ramion długości boku a oraz ramionach długości c są nazywane trójkątami złotymi. Każdy trójkąt równoramienny, którego kąt znajdujący się pomiędzy ramionami jest równy 108° lub 36° jest trójkątem złotym.

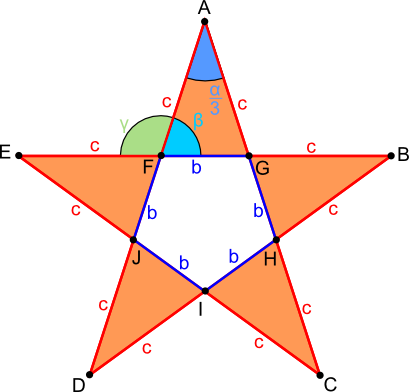
Boki pentagramu można podzielić na mniejsze części c i b tak, jak uczyniłem to ja na rysunku 2. Teraz wystarczy zauważyć, że trójkąty równoramienne o długości ramion c i długości boku b są również trójkątami złotymi, aby móc napisać następującą, prawdziwą równość:

[2]

Zapis wyrażenia w formacie TeX-a:

\frac{p}{a}=\frac{c}{b}=\frac{a}{c}=\frac{c+b}{c}=\frac{2\cdot c+b}{c+b}=\varphi

Powyższe zależności wynikają z istnienia sporej liczby trójkątów złotych w pentagramie wraz z pięciokątem. Dodać tylko mogę, że istnieje taka oto równość, pomiędzy długościami a, b i c:

[3]

Zapis wyrażenia w formacie TeX-a:

a=b+c

Zależność [3] wynika choćby z trójkąta ABH, który jak się okazuje, jest trójkątem złotym co wykazać można badając jego kąty wewnętrzne. Dociekanie tego jakże złożonego zagadnienia pozostawię Czytelnikowi, aby mu się nie nudziło.

Podstawowe wzory

Pięciokąt foremny

Obwód pięciokąta foremnego:

[4]

Zapis wyrażenia w formacie TeX-a:

L = 5\cdot a

Pole powierzchni pięciokąta foremnego można obliczyć z następującego wzoru:

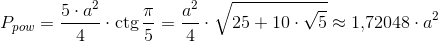[5]

Zapis wyrażenia w formacie TeX-a:

P_{pow} = \frac{5\cdot a^2}{4}\cdot\operatorname{ctg} \frac{\pi}{5} = \frac{a^2}{4}\cdot\sqrt{25+10\cdot\sqrt{5}} \approx 1{\,}72048\cdot a^2

Promień okręgu opisanego na pięciokącie foremnym:

[6]

Zapis wyrażenia w formacie TeX-a:

R_o=\frac{a\cdot\sqrt{50+10\cdot\sqrt{5}}}{10}

Promień okręgu wpisanego w pięciokąt foremny:

[7]

Zapis wyrażenia w formacie TeX-a:

R_w=\frac{a\cdot\sqrt{25+10\cdot\sqrt{5}}}{10}

Długość przekątnej p a zarazem długość boku pentagramu wpisanego w pięciokąt:

[8]

Zapis wyrażenia w formacie TeX-a:

p=\frac{\sqrt{5}+1}{2}\cdot a=\varphi\cdot a

Pentagram

Obwód pentagramu:

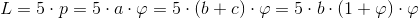[9]

Zapis wyrażenia w formacie TeX-a:

L=5\cdot p=5\cdot a\cdot \varphi=5\cdot\left(b+c\right)\cdot \varphi=5\cdot b\cdot\left(1+\varphi\right)\cdot \varphi

Zależność [9] wynika z zastosowania wzoru [2].

Pole powierzchni pentagramu jest równe polu powierzchni pięciu złotych trójkątów o długości boku równej c:

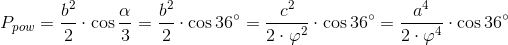[10]

Zapis wyrażenia w formacie TeX-a:

P_{pow}=\frac{b^2}{2}\cdot \cos\frac{\alpha}{3}=\frac{b^2}{2}\cdot \cos 36^\circ=\frac{c^2}{2\cdot\varphi^2}\cdot \cos 36^\circ=\frac{a^4}{2\cdot\varphi^4}\cdot \cos 36^\circ

Również i w zależności [10] swój udział miał wzór [2] i liczba złotego podziału φ.

Grafika żółwia - rysowanie pięciokąta i pentagramu

W Pythonie znajduje się moduł turtle, który umożliwia kreślenie figur geometrycznych. Oto kod programu, który wykreśli pięciokąt foremny:

Z kolei pentagram można wykreślić w sposób następujący:

Można też wykreślić pentagram wraz z pięciokątem:

Więcej na temat pisania programów w Pythonie oraz na temat grafiki żółwia można poczytać na stronie Programowanie → Podstawy Pythona → Grafika żółwia.

Komentarze