Bryły Platońskie
Punkt
Prosta, półprosta i odcinek
Kąt płaski i jego miara
Środek ciężkości figur płaskich
Pole powierzchni
Wielokąty płaskie
Trójkąty - podstawowe cechy i wzory
Twierdzenie Pitagorasa
Twierdzenie o sumie kątów trójkąta dowolnego
Twierdzenie cosinusów (Carnota)
Twierdzenie tangensów (Regiomontana)
Twierdzenie Talesa
Podobieństwo trójkątów i trójkąty przystające
Czworokąty - podstawowe typy i wzory
Pięciokąt foremny i pentagram
Sześciokąt foremny i heksagram
Wielokąty foremne i liczby pierwsze Fermata
Przynależność punktu do wielokąta
Złoty podział odcinka
Koło, okrąg i jego pochodne
Elipsa
Cykloidy
Epicykloidy
Hipocykloidy
Ewolwenta okręgu
Spirala Archimedesa
Objętość
Czworościany
Równoległościany
Prostopadłościany
Graniastosłupy
Ostrosłupy
Bryły Platońskie
Walce
Stożki
Kule, sfery i ich pochodne
Torusy
Bryły obrotowe ograniczone funkcją r(z)
Ta strona należy do działu:
poddziału
Autor podstrony: Krzysztof Zajączkowski
Stronę tą wyświetlono już: 19603 razy
Bryły Platońskie należą do dość szczególnego rodzaju brył, które spełniają następujące warunki:
da się na takiej bryle opisać sferę;
da się w taką bryłę wpisać sferę;
wszystkie boki bryły są przystającymi wielokątami foremnymi. Spełnienie powyższych warunków wymusza również fakt, że każda bryła tego typu będzie należała do zbioru brył wypukłych . Na podstawie powyższych warunków można stwierdzić, że istnieje jedynie 5 brył Platońskich, a są nimi:
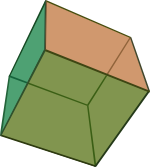
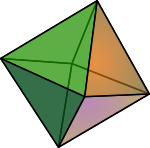
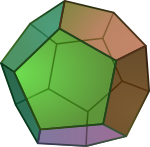
czworościan foremny tetraedr czterech boków o kształcie trójkąta równobocznego ;sześcian foremny heksaedr sześciu boków o kształcie kwadratu ;ośmiościan foremny oktaedr ośmiu boków o kształcie trójkąta równobocznego ;dwunastościan foremny dodekaedr dwunastu boków o kształcie pięciokąta foremnego ;dwudziestościan foremny ikosaedr dwudziestu boków o kształcie trójkąta równobocznego .
Bryły Platońskie zwane foremnymi, kolejno od lewej: a) czworościan foremny (tetraedr); b) sześcian foremny (heksaedr); c) ośmiościan foremny (oktaedr); d) dwunastościan foremny (dodekaedr); e) dwudziestościan foremny (ikosaedr).
Źródło:
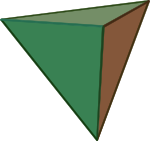
Mała reprodukcja mojego autorstwa pracy Leonarda da Vinci pokazującej tetraedr
Podstawowe cechy
Bryła ta ma 6 krawędzi i 4 wierzchołki a podstawowe jej parametry fizyczne można wyliczyć znając długość krawędzi boków a w następujący sposób:
pole powierzchni wszystkich boków czworościanu:
[1]
Zapis wyrażenia w formacie TeX-a:
S=\sqrt{3}~a^2\approx 1,7321~a^2
objętość bryły:
[2]
Zapis wyrażenia w formacie TeX-a:
V=\frac{\sqrt{2}} {12}~ {a^3}\approx 0,1179~a^3
wysokość h :
[3]
Zapis wyrażenia w formacie TeX-a:
h=a~\frac{\sqrt {24}}{6}=\frac{\sqrt 6}{3}~a\approx 0,8165~a
kąt α nachylenia krawędzi względem ściany, której krawędzią ona nie jest:
[4]
Zapis wyrażenia w formacie TeX-a:
\alpha=\arcsin\frac{\sqrt6}{3}\approx 54,7356^{\circ}"/>
name="[4]
Promień R kuli opisanej na czworościanie foremnym:
[5]
Zapis wyrażenia w formacie TeX-a:
R=\frac{\sqrt{6}} {4}~a\approx 0,6124~a
Promień r kuli wpisanej w czworościanu foremnego:
[6]
Zapis wyrażenia w formacie TeX-a:
r=\frac{\sqrt{6}} {12}~a\approx 0,2041~a
Promień δ kuli stycznej do krawędzi czworościanu foremnego:
[7]
Zapis wyrażenia w formacie TeX-a:
\delta=\frac{1}{4}\cdot a\cdot\sqrt{2}
Kąt między ścianami czworokąta:
[8]
Zapis wyrażenia w formacie TeX-a:
\beta=\arcsin\frac{\sqrt{8}}{3}\approx 70,53^{\circ}
Siatka czworościanu foremnego
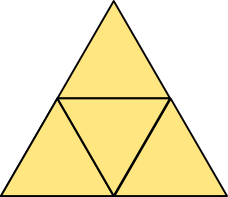
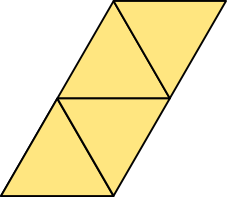
Stosowane są dwie wersje rozwinięcia siatki czworościanu, obie pokazane zostały na poniższym rysunku.
Dwie wersje rozwinięcia siatki czworościanu foremnego
Mała reprodukcja mojego autorstwa pracy Leonarda da Vinci pokazującej heksaedr
Podstawowe cechy
Bryła składa się z 6-ciu przystających ścian kwadratowych , 12-stu krawędzi , 8-miu wierzchołków i czterech przekątnych .
Podstawowe wzory:
Objętość sześcianu:
[9]
Zapis wyrażenia w formacie TeX-a:
V=a^3
Pole powierzchni sześcianu:
[10]
Zapis wyrażenia w formacie TeX-a:
S=6\cdot a
Wzór na promień r kuli wpisanej w sześcian foremny:
[11]
Zapis wyrażenia w formacie TeX-a:
r=\frac{a}{2}
Wzór na promień R kuli opisanej na sześcianie foremnym:
[12]
Zapis wyrażenia w formacie TeX-a:
r=\frac{1}{2}\cdot a\cdot\sqrt{3}
Wzór na promień δ kuli stycznej do krawędzi sześcianu foremnego:
[13]
Zapis wyrażenia w formacie TeX-a:
\delta=a\cdot\frac{\sqrt{2}}{2}
Wzór na długość przekątnej sześcianu:
[14]
Zapis wyrażenia w formacie TeX-a:
d=a\cdot\sqrt{3}
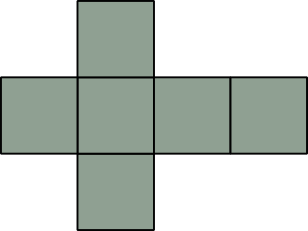
Siatka sześcianu foremnego
Siatka sześcianu foremnego
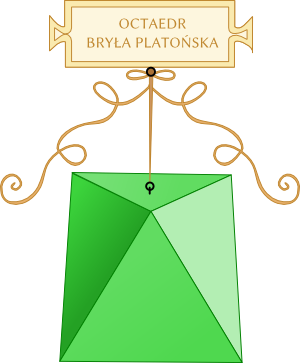
Ośmiościan foremny oktaedr
Mała reprodukcja mojego autorstwa pracy Leonarda da Vinci pokazującej oktaedr
Podstawowe cechy
Bryła ta składa się z ośmiu ścian o kształcie trójkąta równobocznego , 12-stoma krawędzi , 6 wierzchołków oraz 3-ech przekątnych.
Podstawowe wzory:
Objętość ośmiościanu foremnego:
[15]
Zapis wyrażenia w formacie TeX-a:
V=\frac{\sqrt{2}} {3}~a^3\approx 0,4714~a^3
Pole powierzchni bocznej:
[16]
Zapis wyrażenia w formacie TeX-a:
S=2\sqrt{3}~a^2\approx 3,4641~a^2
Promień r kuli wpisanej w ośmiokąt foremny:
[17]
Zapis wyrażenia w formacie TeX-a:
r=\frac{a} {6}\sqrt{6}\approx 0,4082~a
Promień R kuli opisanej na ośmiościanie foremnym:
[18]
Zapis wyrażenia w formacie TeX-a:
R=\frac{a} {2}\sqrt{2}\approx 0,7071~a
Promień δ kuli stycznej do krawędzi ośmiościanu foremnego:
[19]
Zapis wyrażenia w formacie TeX-a:
\delta=\frac{a}{2}
Wysokość h określająca odległość pomiędzy równoległymi ścianami ośmioboku foremnego:
[20]
Zapis wyrażenia w formacie TeX-a:
h=\frac{a} {3}\sqrt{6}\approx 0,8165~a
Długość przekątnej p ośmiościanu foremnego:
[21]
Zapis wyrażenia w formacie TeX-a:
d=a\sqrt{2}\approx 1,4142~a
Kąt pomiędzy ścianami:
[22]
Zapis wyrażenia w formacie TeX-a:
\alpha =2~\operatorname{arcsin}\sqrt{\frac{2}{3}}\approx 109^{\circ}
gdzie Φ oznacza liczbę złotą , której wartość wynosi około: 1,6180339887...
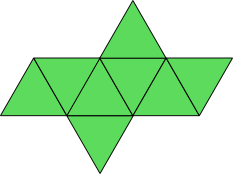
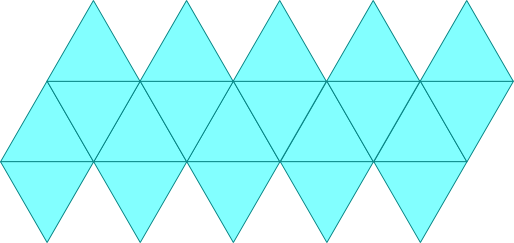
Siatka ośmiościanu foremnego
Dwie wersje siatki ośmiościanu foremnego
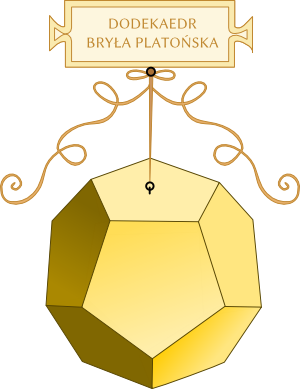
Dwunastościan foremny dodekaedr
Mała reprodukcja mojego autorstwa pracy Leonarda da Vinci pokazującej dodekaedr
Podstawowe cechy
Bryła składa się z 12-stu przystających ścian w kształcie pięciokąta foremnego , 30-stu krawędzi , 20-stu wierzchołków .
Podstawowe wzory:
Wzór na objętość:
[23]
Zapis wyrażenia w formacie TeX-a:
V=\frac{5\cdot \Phi^2}{6-2\cdot\Phi}\cdot a=\frac{1} {4}~a^3~(15+7\sqrt{5})\approx 7,6613~a^3\delta=\frac{a\cdot \left(3+\sqrt{3}\right)}{4}
Wzór na pole powierzchni bocznej:
[24]
Zapis wyrażenia w formacie TeX-a:
S=\frac{15\cdot\Phi}{\sqrt{3-\Phi}}=3\cdot a^2~\sqrt{5\cdot (5+2\sqrt{5})}\approx 20,6457~a^2
Wzór na promień r kuli wpisanej w dwunastościan foremny:
[25]
Zapis wyrażenia w formacie TeX-a:
r=\frac{a} {20}\sqrt{10(25+11\sqrt{5})}\approx 1,1135~a
Wzór na promień R kuli opisanej na dwunastościanie foremnym:
[26]
Zapis wyrażenia w formacie TeX-a:
R=\frac{a} {4}~\sqrt{3}~(1+\sqrt{5})\approx 1,4013~a
Wzór na promień δ kuli stycznej do krawędzi dwunastościanu foremnego:
[27]
Zapis wyrażenia w formacie TeX-a:
\delta=\frac{a\cdot \left(3+\sqrt{3}\right)}{4}
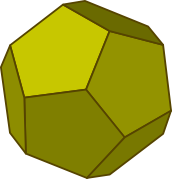
Dwunastościan foremny można wpisać w dwudziestościan foremny w sposób pokazany na rysunku 10
Po lewej: dwudziestościan foremny; po prawej: dwunastościan foremny wpisany w dwudziestościan
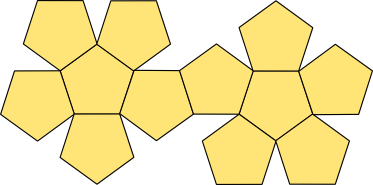
Siatka dwunastościanu foremnego
Siatka dwunastościanu foremnego
Stosunek długości krawędzi dwudziestościanu foremnego do dwunastościanu wynosi:
[28]
Zapis wyrażenia w formacie TeX-a:
\frac{\Phi}{\sqrt{5}}
Kąt pomiędzy ścianami dwunastościanu foremnego wynosi:
[29]
Zapis wyrażenia w formacie TeX-a:
\alpha=116,6^{\circ}
Dwudziestościan foremny ikosaedr
Podstawowe cechy
Bryła składa się z 20-stu przystających boków w kształcie trójkąta foremnego , 30 krawędzi , 12 wierzchołków i 15 płaszczyzn symetrii .
Podstawowe wzory:
Objętość bryły:
[30]
Zapis wyrażenia w formacie TeX-a:
V=\frac{5\cdot\Phi^2}{6}=\frac{5} {12}\cdot a^3~(3+\sqrt{5})\approx 2,1817\cdot a^3
Powierzchnia boczna:
[31]
Zapis wyrażenia w formacie TeX-a:
S=5\cdot a^2\sqrt{3}\approx 8,6603\cdot a^2
Promień r kuli wpisanej w dwudziestościan foremny:
[32]
Zapis wyrażenia w formacie TeX-a:
r=\frac{a} {12}\cdot\sqrt{3}\cdot\left(3+\sqrt{5}\right)\approx 0,7558\cdot a
Promień R kuli opisanej na dwudziestościanie foremnym:
[33]
Zapis wyrażenia w formacie TeX-a:
R=\frac{a}{4}\cdot\sqrt{10+2\cdot\sqrt{5}}\approx 0,9511\cdot a
Promień δ styczny do krawędzi dwudziestościanu foremnego:
[34]
Zapis wyrażenia w formacie TeX-a:
\delta=\frac{a\cdot\left(1+\sqrt{5}\right)}{4}
Wysokość h pomiędzy równoległymi płaszczyznami dwudziestościanu foremnego:
[35]
Zapis wyrażenia w formacie TeX-a:
h=2\cdot r=\frac{a}{6}\cdot\sqrt{3}\cdot\left(3+\sqrt{5}\right)\approx 1,5115\cdot a
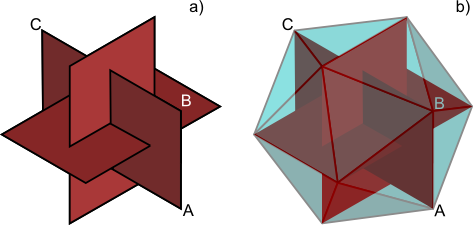
Ciekawostką niech będzie fakt, że dwudziestościan foremny da się opisać na trzech wzajemnie się przecinających pod kątem 90° prostokątach złotych tak jak widoczne jest to na poniższym rysunku.
Dwudziestościan foremny opisany na trzech wzajemnie się przecinających pod kątem pod kątem 90° prostokątach złotych
Siatka dwudziestościanu foremnego
Siatka dwudziestościanu foremnego
Tematy powiązane


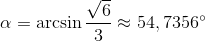



![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_2547.gif)


![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_2548.gif)
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_2549.gif)

![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_2555.gif)
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_2557.gif)
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_2558.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_2565.gif)


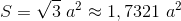
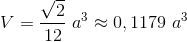
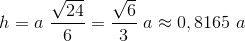
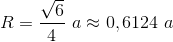
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2536.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2566.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2537.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2538.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2539.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2562.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_2563.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_2564.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_2540.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_2541.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_2542.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_2543.gif)
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_2544.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_2561.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_2545.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_2546.gif)
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_2550.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_2551.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_2552.gif)
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_2553.gif)
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_2554.gif)
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_2556.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_2559.gif)