Spirala Archimedesa

Stronę tą wyświetlono już: 15063 razy

Opis matematyczny

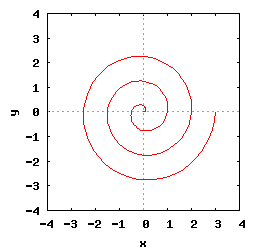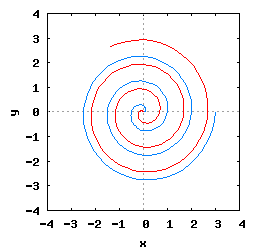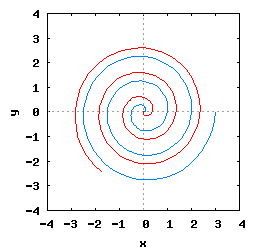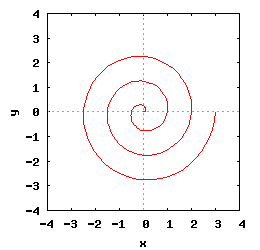
Spirala Archimedesa jest krzywą, którą można zapisać w współrzędnych biegunowych w następującej postaci:

[1]

Zapis wyrażenia w formacie TeX-a:

R(\varphi)=\frac{\left(k\cdot\varphi+\Delta k\right)}{2\cdot\pi}\cdot\left(\varphi+\Delta\varphi\right)

gdzie:

• φ - zmienna kąta wyrażonego w radianach;
• R(φ) - funkcja zależności promienia od kąta φ;
• k - parametr określający przyrost odległości pomiędzy poszczególnymi zwojami spirali Archimedesa;
• Δk - parametr przesuwający promień wodzący funkcji o zadaną wartość;
• Δφ - parametr przesuwający kąt początkowy spirali Archimedesa

Równania parametryczne spirali Archimedesa:

[2]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} x=\cfrac{k\cdot\varphi+\Delta k}{2\cdot\pi}\cdot\sin\left(\varphi+\Delta\varphi\right)+\Delta x \\ y= \cfrac{k\cdot\varphi+\Delta k}{2\cdot\pi}\cdot\cos\left(\varphi+\Delta\varphi\right)+\Delta y\end{cases}

gdzie:

• Δx - przemieszczenie w osi x;
• Δy - przemieszczenie w osi y.

a)b)c)d)

Wzory

Istnieje możliwość obliczenia pola powierzchni pod wykresem spirali Archimedesa dla zakresu kątów od φ₁ do φ₂, gdzie φ₂-φ₁≤2π oraz φ₁≤φ₂.

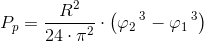[3]

Zapis wyrażenia w formacie TeX-a:

P_p=\frac{R^2}{24\cdot\pi^2}\cdot\left(\varphi_2\,^3-\varphi_1\,^3\right)

gdzie:

• R - odległość pomiędzy sąsiadującymi zwojami spirali Archimedesa;
• φ₁ - kąt początkowy spirali Archimedesa;
• φ₂ - kąt końcowy spirali Archimedesa

Zastosowanie spirali Archimedesa

W technice spirala Archimedesa ma zastosowanie w obrabiarkach nazywanych tokarkami. Ściślej rzecz ujmując w uchwycie tokarskim znajduje się spirala Archimedesa, która odpowiedzialna jest za równomierne przesuwanie szczęk tego uchwytu jak widać na załączonym ponirzej rysunku.

Spirala Archimedesa ma pewne mafijne powiązanie z problemem kwadratury koła, który oczywiście jest nierozwiązywalny przy użyciu cyrkla i linijki. Czym jest kwadratura koła? Z najdzikszą rozkoszą odpowiem, że jest to problem wyznaczenia długości boku kwadratu, takiego, że jego pole powierzchni odpowiada polu powierzchni koła o promieniu R. Jeżeli chodzi o spiralę Archimedesa, to linia styczna do jej krzywej w punkcie A z poniższego rysunku wyznacza trójkąt OAB, którego długość boku OA jest równa promieniowi R, a długość boku OB jest równa 2·π·R. Co ciekawe pole powierzchni tego trójkąta jest równe polu powierzchni okręgu o promieniu R, jednakże nas interesuje wyznaczenie długości boku kwadratu, a do tego celu potrzebna jest połowa długości OB powiększona o długość OA. Tak otrzymany odcinek należy podzielić na pół aby w końcu otrzymać długość boku kwadratu, którego pole powierzchni jest równe polu powierzchni koła o promieniu R.

Grafika żółwia - kreślenie spirali Archimedesa

W Pythonie jest moduł o nazwie turtle, który umożliwia pisanie programów rysujących różne figury geometryczne. Oto prosty przykład programu rysującego spiralę Archimedesa:

Więcej na temat pisania programów w Pythonie oraz na temat grafiki żółwia można poczytać na stronie Programowanie → Podstawy Pythona → Grafika żółwia.

Komentarze