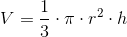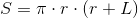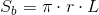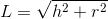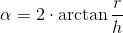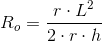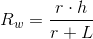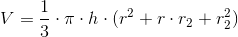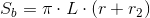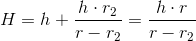Stożki
Stronę tą wyświetlono już: 20978 razy
Definicja stożka
Stożek prosty to bryła powstała w wyniku obrotu płaszczyzny trójkąta prostokątnego o kąt 360° względem osi przechodzącej przez jedną z przyprostokątnych tego trójkąta.
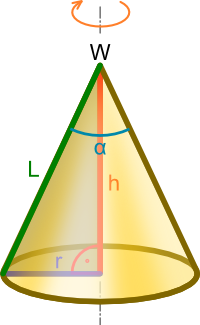
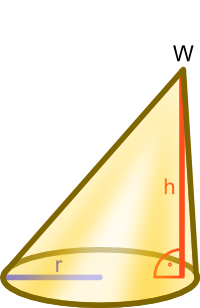
Opis oznaczeń:
- h wysokość stożka;
- r - promień podstawy stożka.
- L - tworząca stożka.
- α - kąt rozwarcia stożka
Opis stożka prostego w kartezjańskim układzie współrzędnych
Stożek prosty można opisać następującymi nierównościami:
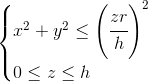 | [1] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- promień r > 0;
- wysokość h > 0.
Parametryczny zapis funkcji powierzchni stożka prostego:
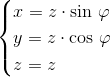 | [2] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- φ zawiera się w przedziale od 0 do 2·π;
- z zawiera się w przedziale od 0 do h.
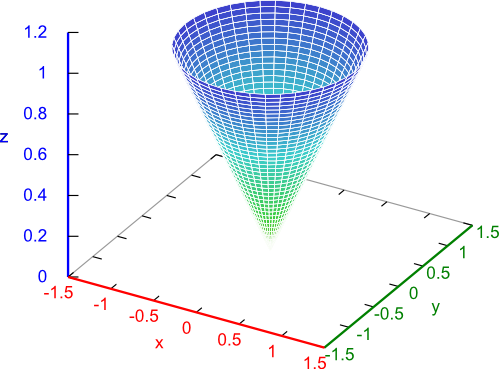
Przykład wygenerowanej płaszczyzny stożka za pomocą programu wxMaxima:
Edytowany w programie Inkscape.
Podstawowe wzory
Objętość stożka dowolnego
Zarówno dla stożka prostego jak i pochyłego objętość można obliczyć z następującego wzoru:
gdzie:
- r - promień podstawy stożka;
- h - wysokość stożka.
Wyznaczaniem powyższego wzoru za pomocą całek zajmowałem się w zadaniu 1 na podstronie działu Matematyka → Całki oznaczone.
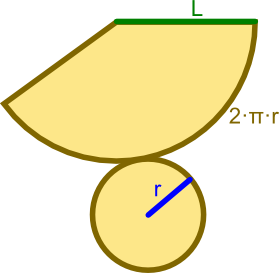
Pole powierzchni
Dla stożka prostego pole powierzchni można obliczyć korzystając z wzoru:
gdzie:
- r - promień stożka;
- L - długość tworzącej stożka.
Pole powierzchni bocznej stożka prostego:
Długość tworzącej L stożka prostego
Tworzącą L można a czasem nawet i trzeba obliczyć z następującego wzoru:
Kąt α rozwarcia stożka prostego
Kąt rozwarcia α jest kątem przywierzchołkowym W poprzecznego osiowego przekroju stożka, wzór na ów kąt jest następujący:
Promień kuli opisanej na stożku prostym
Promień kuli wpisanej w stożek prosty
Przekroje stożka
Ścięcie stożka prostego płaszczyzną przechodzącą przez oś symetrii
Wynikiem ścięcia stożka płaszczyzną przechodzącą przez oś symetrii jest oczywiście trójkąt równoramienny.
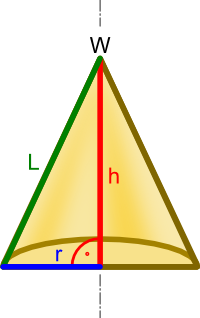
Ścięcie stożka prostego płaszczyzną przechodzącą przez wierzchołek W
W wyniku przecięcia stożka prostego dowolną płaszczyzną taką, że wierzchołek W tego stożka należy do tej płaszczyzny skutkuje otrzymaniem trójkąta równoramiennego.
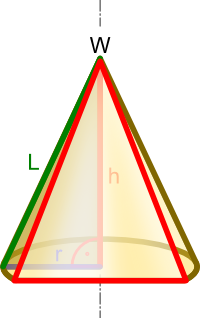
Ścięcie stożka prostego płaszczyzną równoległą do podstawy
Wynikiem ścięcia stożka prostego płaszczyzną równoległą do jego podstawy jest okrąg.
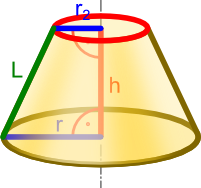
Wynikiem takiego zabiegu otrzymuje się bryłę nazywaną stożkiem ściętym, która również jest bryłą obrotową uzyskaną w wyniuku obrotu trapezu prostokątnego względem osi przechodzącej przez jego bok znajdujący się przy obu kątach prostych tego trapezu.
Ścięcie stożka płaszczyzną pod kątem mierzonym względem osi symetrii większym niż połowa kąta jego rozwarcia α
Wynikiem takiego potraktowania stożka będzie płaszczyzna o zarysie eliptycznym.
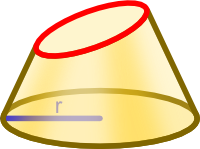
Ścięcie stożka płaszczyzną pod kątem mierzonym względem osi symetrii równym połowie kąta jego rozwarcia α
Wynikiem takiego ścięcia jest płaszczyzna o zarysie paraboli.
Ścięcie stożka płaszczyzną pod kątem mierzonym względem osi symetrii większym niż połowa kąta jego rozwarcia α
Wynikiem takiego ścięcia jest płaszczyzna o zarysie hiperboli.

Stożek ścięty - podstawowe wzory

- r - średnica podstawy dolnej;
- r2 - średnica podstawy górnej;
- h - wysokość
Objętość stożka ściętego
Pole powierzchni bocznej
Wysokość stożka przed ścięciem
Długość tworzącej stożka
Rozwinięcie siatki ostrosłupa prostego