Bryły obrotowe ograniczone funkcją r(z)
Stronę tą wyświetlono już: 6232 razy
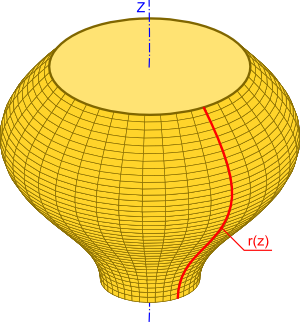
Ogólna definicja brył obrotowych
Każda bryła, której wszystkie punkty znajdują się w odległości od pewnej osi nie większej niż pewna dana funkcja r(z) jest bryłą obrotową, gdzie z określa położenie na osi obrotu, zaś r(z) funkcję promienia płaszczyzny dla danego położenia z.
Z powyższego wynika, że musi być spełniona następująca nierówność dla bryły obrotowej, przy założeniu, że osią jest oś z układu współrzędnych kartezjańskich, której maksymalny promień r opisuje funkcja r(z).
Wzór [1] dla walca
Jako że walec jest również bryłą obrotową, dla której funkcja r(z) jest równa promieniowi podstawy R tegoż walca, tak więc walec opisuje następująca nierówność:
Wzór [1] dla stożka
Także i stożek jest bryłą obrotową, dla której funkcja r(z) jest równa:
gdzie:
- R - promień podstawy stożka;
- h - wysokość stożka.
Nierówności opisujące stożek będzie więc miała postać następującą:
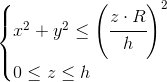 | [4] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- promień r > 0;
- wysokość h > 0.
Wzór [1] dla kuli
Nie będzie wielkim zaskoczeniem, gdy napiszę, że kula jest bryłą obrotową, dla której funkcja r(z) jest równa:
gdzie:
- R - promień kuli;
Nierówności opisujące walec będzie więc miała postać następującą:
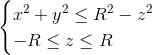 | [6] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- promień r > 0;
- wysokość h > 0.
Ogólny wzór na objętość dowolnej bryły obrotowej ograniczonej funkcją r(z)
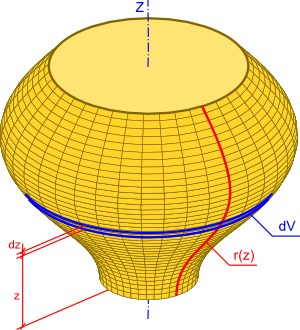
Objętość bryły obrotowej jest równa całce iloczynu pola powierzchni okręgu o promieniu danym funkcją r(z) i jej elementarnej wysokości dz.
Oznaczenia:
- z - położenie przekroju bryły;
- dz - elementarna wysokość przekroju;
- dv - elementarna objętość, która jest równa π·r(z)2·dx;
- r(z) - funkcja promienia r przekroju i jego położenia na osi z.
Przykład zastosowanie wzoru [7] dla walca
Wyznaczenie wzoru na objętość walca będzie banalnie proste:
![Wyznaczenie wzoru na objętość walca za pomocą wzoru [7]](https://obliczeniowo.com.pl/rownania/w_2752.gif) | [8] |
Zapis wyrażenia w formacie TeX-a:
Przykład zastosowanie wzoru [7] dla stożka
Wyznaczenie wzoru na objętość stożka będzie równie banalnie proste co walca:
![Wyznaczenie wzoru na objętość stożka za pomocą wzoru [7]](https://obliczeniowo.com.pl/rownania/w_2753.gif) | [9] |
Zapis wyrażenia w formacie TeX-a:
Przykład zastosowanie wzoru [7] dla kuli
Wyznaczenie wzoru na objętość kuli:

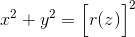


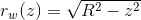
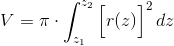
![Wyznaczenie wzoru na objętość kuli za pomocą wzoru [7]](https://obliczeniowo.com.pl/rownania/w_2754.gif)