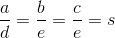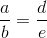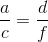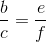Stronę tą wyświetlono już: 7701 razy

Dwa trójkąty ABC i DEF są podobne gdy spełniona jest następująca równość:

[1]

Zapis wyrażenia w formacie TeX-a:

\frac{a}{d}=\frac{b}{e}=\frac{c}{e}=s

gdzie s jest wielkością liczbową pozbawioną jednostki określającą skalę podobieństwa trójkątów ABC i DEF.

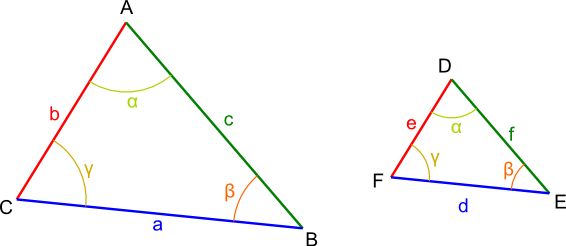
Dużo prościej rzecz ujmując: dwa trójkąty są podobne, gdy kąty wewnętrzne znajdujące się w jednym z nich odpowiadają wartościom kątów w drugim (co widać na rysunku 1 jak na dłoni).

Podobieństwo trójkątów jest tutaj bardzo mocno powiązane z omawianym wcześniej twierdzeniem Talesa, ponieważ zachodzą tutaj następujące równości:

[2]

Zapis wyrażenia w formacie TeX-a:

\frac{a}{b}=\frac{d}{e}

[3]

Zapis wyrażenia w formacie TeX-a:

\frac{a}{c}=\frac{d}{f}

[4]

Zapis wyrażenia w formacie TeX-a:

\frac{b}{c}=\frac{e}{f}

Z wyżej wymienionych proporcji często-gęsto się korzysta w celu wyznaczenia długości boków trójkątów podobnych i z tego względu ważna jest umiejętność stwierdzenia, że dane dwa trójkąty są trójkątami podobnymi. Takich sposobów istnieje trzy:

1. gdy kąty zawarte w trójkącie ABC odpowiadają wartościom kątów zawartych w trójkącie DEF to takie trójkąty są podobne (również gdy znane są dwa dowolne kąty, które są odpowiednio równe) - cecha kąt - kąt - kąt
2. gdy stosunki długości dwóch par boków oraz miara kąta zawartego między nimi są sobie równe - cecha bok - kąt - bok;
3. gdy stosunki długości par boków trójkątów są sobie równe (wzór [1]) - cecha bok - bok - bok

Gdy skala podobieństwa s dla dwóch danych trójkątów jest równa 1 to takie trójkąty nazywane są przystającymi. Można stwierdzić, że dwa trójkąty są przystające gdy:

1. dwa kąty oraz długość jednego boku w jednym trójkącie są takie same co w drugim - cecha kąt - bok - kąt;
2. długości dwóch boków i kąta zawartego pomiędzy nimi w jednym trójkącie są takie same co w drugim - cecha bok - kąt - bok
3. długości boków trójkąta pierwszego odpowiadają długościom boków trójkąta drugiego - cecha bok - bok - bok