Prosta, półprosta i odcinek
Stronę tą wyświetlono już: 78208 razy
Podstawowe właściwości i definicje
Prosta jest to linia, która nie ma ani początku ani końca. Zdefiniować prostą można na wiele różnych sposobów, ale o tym napiszę nieco później. Długość prostej jest nieskończona.
Półprosta jest równa połowie prostej, na której ona leży. Półprosta ma punkt początkowy, ale nie ma końca (ciągnie się w nieskończoność). O ile prostą można podzielić na dwie równe części poprzez obranie na niej dowolnego punktu o tyle półprostej nie da się podzielić w ten sposób. Długość półprostej jest nieskończona.
Odcinek - jest to wycinek prostej, który ma punkt początkowy i końcowy. Długość każdego odcinka jest zawsze wielkością skończoną, a więc należy do zbioru liczb rzeczywistych dodatnich. Każdy odcinek da się podzielić na równe części a co za tym idzie proces ten można powtarzać w nieskończoność.
Każda prosta, półprosta jak i odcinek wydzielają pewien nieskończony zbiór punktów. Inaczej rzecz ujmując, na każdej prostej, półprostej czy odcinku leży nieskończenie wiele punktów.
Opis prostej
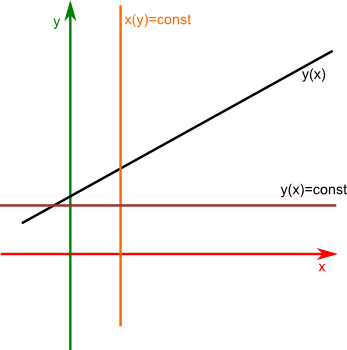
Każdą prostą można opisać na kilka różnych sposobów. Jednym z nich jest opis funkcyjny np. w przestrzeni 2W funkcją y(x), przy czym funkcją tą nie można opisać prostych prostopadłych do osi x, do zdefiniowania takiej prostej trzeba użyć funkcji odwrotnej x(y).
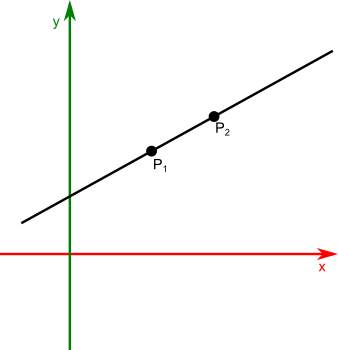
Prostą można również opisać za pomocą dwóch punktów, przez które ta prosta przechodzi, albowiem przez dwa dowolnie obrane ale nie pokrywające się punkty przechodzi tylko jedna prosta.
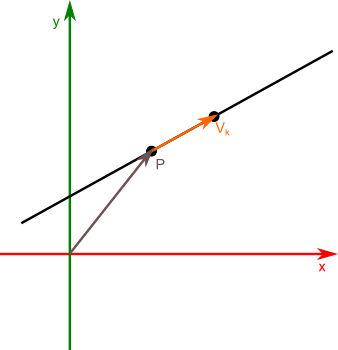
Na koniec, prostą można zdefiniować za pomocą jednego punktu leżącego na tej prostej oraz wektora kierunkowego prostej.
Opis półprostej
Każda półprosta leży na jakiejś jednej prostej, a więc wszystkie typy opisu prostej w pewien sposób opisują również i półprostą. Tutaj jednak konieczne jest jeszcze wskazanie punktu początkowego półprostej oraz kierunku.
Jeżeli więc półprosta jest opisana funkcją y(x) to trzeba jeszcze wskazać taki x, dla którego odpowiada punkt początkowy prostej oraz określić jej kierunek jako x≥xp, gdzie xp określa punkt początkowy półprostej. Odwrotnie dla półprostej przeciwnie skierowanej, czyli x≤xp.
W przypadku dwóch punktów, przez które półprosta przechodzi, pierwszy punkt niech wskazuje punkt początkowy, natomiast drugi kierunek i zwrot półprostej.
W przypadku punktu zaczepienia i wektora kierunkowego można zadziałać w analogiczny sposób jak w przypadku dwóch punktów.
Opis odcinka
Odcinek można również opisać za pomocą funkcji y(x) w takim jednak przypadku należy podać wartości x-sów odpowiadających początkowi i końcowi takiego odcinka.
Odcinek można również zdefiniować za pomocą dwóch punktów wyznaczających jego końce.
Odcinek można opisać punktem zaczepienia oraz wektorem kierunkowym długości równej długości samego odcinka.
Uwaga! Wektor kierunkowy we wszystkich przypadkach nie może być wektorem zerowym. W przypadku definiowania prostej, półprostej czy odcinka za pomocą dwóch punktów, punkty te nie mogą się pokrywać.
Długość odcinka
Długość odcinka danego punktami P1 i P2 można obliczyć za pomocą następującego wzoru:
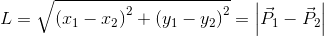 | [1] |
Zapis wyrażenia w formacie TeX-a:
W przypadku, gdy dany jest punkt zaczepienia Pz i wektor kierunkowy Vk wystarczy obliczyć długość wektora Vk w następujący sposób:
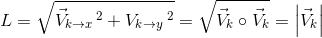 | [2] |
Zapis wyrażenia w formacie TeX-a:
W przypadku, gdy odcinek dany jest funkcją y(x) oraz wartościami x1 i x2 to jego długość liczy się za pomocą wzoru:
![L=sqrt{left(x_1-x_2right)^2+left[yleft(x_1right)-yleft(x_2right)right]^2}](https://obliczeniowo.com.pl/rownania/w_1995.gif) | [3] |
Zapis wyrażenia w formacie TeX-a:
Wzory [1], [2] i [3] można rozszerzyć o składową z dzięki czemu możliwe będzie obliczenie długości odcinka w przestrzeni 3W.
Prostopadłość
Dla dwóch dowolnych prostych lub półprostych czy odcinków można wykonać za pomocą cyrkla i linijki sprawdzenie, czy są one względem siebie prostopadłe. Prostopadłość oznacza, że kąt pomiędzy rozpatrywanymi obiektami prostoliniowymi jest równy 90°.
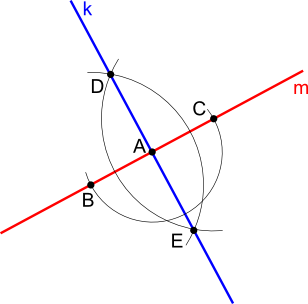
Obierzmy więc sobie dwie proste k i m takie jak na rysunku 5, które przecinają się w punkcie A. Z punktu A dowolną szerokością cyrkla należy wyznaczyć punkty B oraz C z tych zaś punktów należy zakreślić promieniem większym niż odległość |AB| łuk z punktu B i C otrzymując tym samym punkty D i E. Jeżeli prosta k leży na tych punktach, to jest ona prostopadła do prostej m.
Z konstrukcji z rysunku 5 korzysta się również w celu wyznaczenia prostej prostopadłej w punkcie A.
Prostopadłość można sprawdzić za pomocą wzoru [1] z strony Matematyka → Wektory → Iloczyn skalarny.
Równoległość
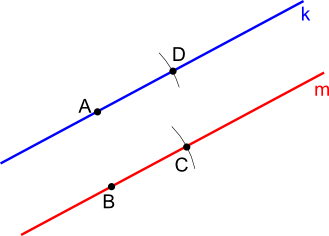
Dwa prostoliniowe obiekty k i m są względem siebie równoległe, jeżeli odległość pomiędzy nimi się nie zmienia. Innymi słowy, jeżeli obiorę sobie dwa dowolne punkty A na prostej k oraz B na prostej m i dowolną rozwartością cyrkla wyznaczę z punktów A i B punkty C i D, z których odmierzona cyrklem odległość |CD| musi być równa odległości |AB|.
Z powyższego wynika niezbicie, że dwie proste są równoległe, gdy nie mają punktu przecięcia lub mają ich nieskończenie wiele (pokrywają się). A więc, gdy proste mają punkt przecięcia to nie są równoległe.
Równoległość można również sprawdzić obierając dwa dowolne ale nie pokrywające się punkty na prostej k i prostej m oraz wykorzystując wzory [1] i [8] z strony Matematyka → Wektory → Wyznacznik dwóch wektorów.