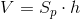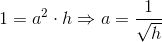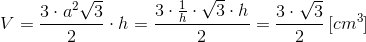Graniastosłupy
Stronę tą wyświetlono już: 7485 razy
Definicja
Graniastosłupy należą do grupy brył 3W, których dwie równoległe względem siebie płaszczyzny są wielokątami przystającymi (zwanymi podstawami graniastosłupa), zaś płaszczyzny boczne są prostokątami lub równoległobokami, których wszystkie wierzchołki są także wierzchołkami podstaw.
Graniastosłupem n-kątnym nazywa się graniastosłup, którego podstawy są n-kątami.
Wysokość h graniastosłupa to najkrótsza odległość dzieląca podstawy graniastosłupa
Podział graniastosłupów
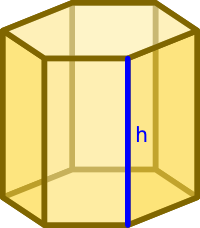
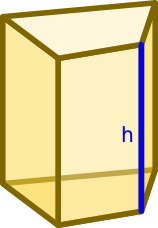
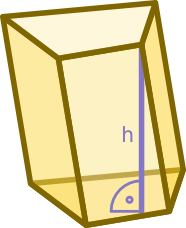
Drodzy czytelnicy, graniastosłupy to obszerna grupa brył 3W. Zalicza się do nich następujące bryły, które już wcześniej zostały omówione:
Prostopadłościany jak i sześciany należą do grupy graniastosłupów zwanych prawidłowymi.
Graniastosłup prawidłowy to graniastosłup prosty, którego podstawy są wielokątami foremnymi.
Graniastosłupy dzieli się na:
- proste, których wszystkie ściany boczne są prostokątami, a krawędzie boczne są prostopadłe do podstaw graniastosłupa;
- pochyłe, których część lub wszystkie powierzchnie boczne są równoległobokami nie będącymi prostokątami, a krawędzie boczne tworzą kąt z płaszczyznami podstaw różny od 90°.
Podstawowe wzory
Dla graniastosłupa dowolnego:
Ogólny wzór na objętość graniastosłupa dowolnego, gdy dane jest pole jego podstawy Sp oraz wysokość h:
Dla graniastosłupów trójkątnych
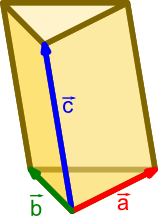
Oznaczanie:
- a, b, c - wektory wychodzące z jednego wierzchołka graniastowłupa trójkątnego.
Szczególnym przypadkiem graniastosłupa jest graniastosłup trójkątny, a to dlatego, że można jego objętość obliczyć z następującego wzoru:
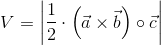 | [2] |
Zapis wyrażenia w formacie TeX-a:
Gdy dana jest wysokość h graniastosłupa trójkątnego powyższy wzór upraszcza się do postaci:
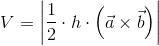 | [3] |
Zapis wyrażenia w formacie TeX-a:
Możliwe jest również obliczenie pola powierzchni graniastosłupa trójkątnego:
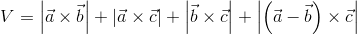 | [4] |
Zapis wyrażenia w formacie TeX-a:
Zadania z graniastosłupami
Zadanie 1
Oblicz objętość graniastosłupa prawidłowego o podstawie sześciokąta, którego wysokość h jest równa promieniowi R kuli opisanej na tym graniastosłupie jeżeli wiadomo, że objętość tejże kuli jest równa 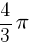 [cm3].
[cm3].
Wzór na objętość kuli można znaleźć na stronie Matematyka → Geometria → Kule, sfery i ich pochodne i jest to wzór [5]. Dzięki niemu można wyznaczyć promień R kuli opisanej na sześcianie w następujący sposób:
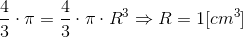 | [5] |
Zapis wyrażenia w formacie TeX-a:
Do dalszej części zadania przyda się poniższy rysunek pomocniczy.
Wystarczy zauważyć, że długość głównej przekątnej graniastosłupa prawidłowego o podstawie sześcianu jest równy dwukrotności promienia R kuli na nim opisanej. Znając tą zależność można wyznaczyć korzystając z starego dobrego twierdzenia Pitagorasa długość krawędzi a sześciokąta foremnego, który znajduje się w jego podstawie i który jest jednocześnie promieniem okręgu na nim opisanego. A więc szukana długość boku a będzie równa:
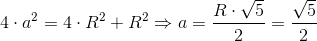 | [6] |
Zapis wyrażenia w formacie TeX-a:
Objętość graniastosłupa prawidłowego o podstawie sześciokąta można więc już obliczyć w następujący sposób:
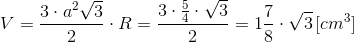 | [7] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 2
Oblicz objętość graniastosłupa prawidłowego o podstawie sześciokąta, którego wysokość h jest dana i równa wysokości graniastosłupa prawidłowego o podstawie kwadratu, jeżeli wiadomo, że objętość tego graniastosłupa jest równa 1 [cm3] a długość krawędzi podstawy a obu graniastosłupów jest taka sama.
Dla graniastosłupa prawidłowego o podstawie kwadratu można zapisać następującą równość:
Przypominam, że h jest dane. Tak więc objętość graniastosłupa o podstawie sześcianu będzie równa: