Stronę tą wyświetlono już: 23398 razy

Każdemu n wymiarowemu wektorowi przyporządkowana jest pewna liczba (skalar), który określany jest jako wartości, długość lub moduł danego wektora.

Ogólny wzór, umożliwiający wyznaczenie modułu wektora przyjmuje następującą postać:

[1]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{a}\right|=\sqrt{\sum_{i=1}^{n}{{a_{i}}^2}}

gdzie:

jest oznaczeniem długości wektora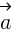

Dla wektora 2W wzór [1] przyjmuje postać, którą z pewnością każdy z Was jest w stanie powiązać z twierdzeniem Pitagoras:

[2]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{a}\right|=\sqrt{{a_{x}}^2+{a_{y}}^2}

Dla wektora 3W wzór [1] z kolei przyjmuje postać (wynikającą również z zastosowania twierdzenia Pitagorasa):

[3]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{a}\right|=\sqrt{{a_{x}}^2+{a_{y}}^2+{a_{z}}^2}

Operacje nie wpływające na długość wektora

1. Każdy obrót wektora względem dowolnego punktu w przestrzeni o wymiarze n≥2 nie wpływa na długość wektora.
2. Każde odbicie lustrzane względem dowolnie ułożonej osi w układach o wymiarze n≥2 nie wpływa na długość wektora.
3. Każde odbicie lustrzane względem dowolnie ułożonej płaszczyzny 2W w układach o wymiarze n≥3 nie wpływa na długość wektora.
4. Każde odbicie lustrzane względem dowolnie ułożonej hiperpłaszczyzny o wymiarze <n w układach o wymiarze n≥4 nie wpływa na długość wektora.

Operacje wpływające tylko na długość wektora

Istnieje tylko jedna operacja, która nie zmieniając kierunku wektora jest w stanie zmieniać jego wartość. Tą operacją jest mnożenie wektora przez skalar, przy czym gdy wektor mnożony jest przez skalar o wartości ujemnej to w takim przypadku zmienia się nie tylko wartość, ale i zwrot wektora na przeciwny.