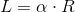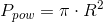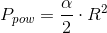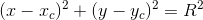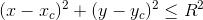Koło, okrąg i jego pochodne

Stronę tą wyświetlono już: 7738 razy

Podstawowe definicje i pojęcia

Okręgiem nazywa się wszystkie punkty równoodległe o wartość promienia R od pewnego punktu S_c zwanego środkiem okręgu. Każdy okrąg charakteryzuje: obwód, średnica i promień. Okrąg nie ma wypełnienia a więc nie ma też pola powierzchni.

Kołem nazywa się wszystkie punkty znajdujące się w odległości co najwyżej pewnej wartości promienia R od pewnego punktu S_c zwanego środkiem okręgu. Każde koło posiada wszystkie cechy okręgu, z tą tylko różnicą, że koło ma wypełnienie a więc i pole powierzchni.

Cięciwa jest to odcinek łączący dwa punkty na obwodzie koła lub okręgu.

Średnica d jest to odcinek łączący dwa punkty na obwodzie koła lub okręgu i przechodzący przez ich środek S_c.

Środek okręgu S_c wspomniany już wcześniej jest również środkiem ciężkości okręgu, przez który przechodzi pęk nieskończonej liczby osi symetrii okręgu.

Wycinek koła jest to figura geometryczna składająca się z łuku kolistego oraz dwóch prostokreślnych boków o długości równej promieniowi R łuku kolistego stanowiącego jeden z boków tej figury. Każdy wycinek koła w odróżnieniu od koła czy też okręgu ma jedną i tylko jedną oś symetrii.

Odcinek koła to figura płaska, powstała w wyniku ścięcia koła pewną prostą przechodzącą przez dwa punkty takiego koła. W wyniku takiej operacji ścięcia okręgu otrzymuje się figurę składającą się z łuku kolistego i odcinka prostoliniowego c.

Łuk to wycinek okręgu, a więc nie ma on pola powierzchni, ma za to jedną oś symetrii, środek S łuku, promień łuku R, początek i koniec. Łuk ma długość, którą można obliczyć znając jego kąt α i promień R

Podstawowe wzory

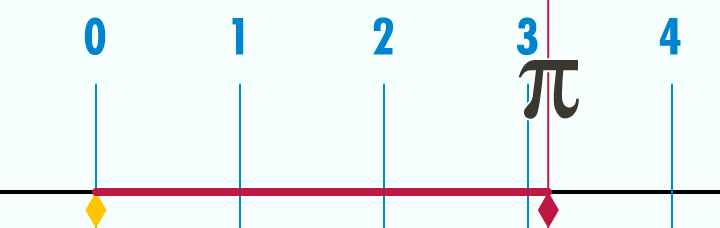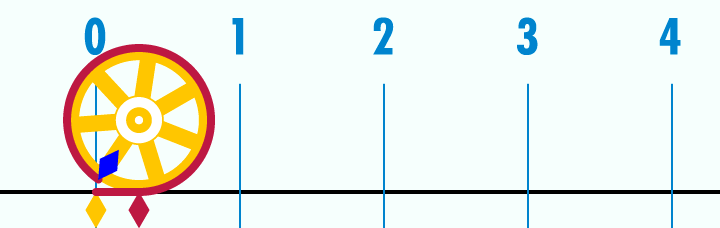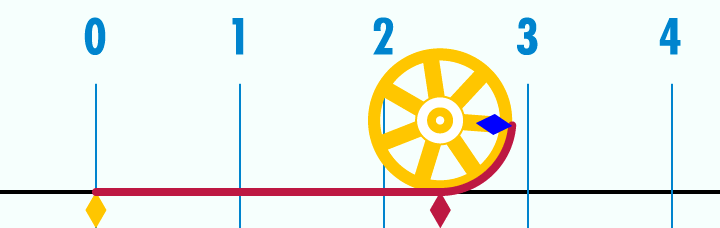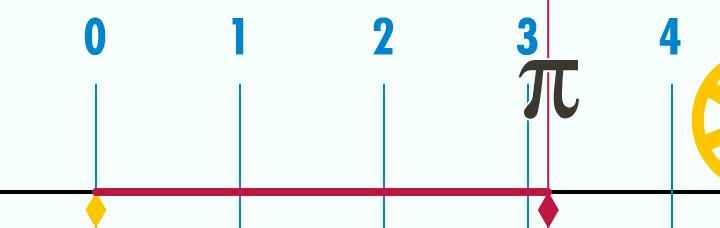
W celu obliczenia obwodu okręgu czy też koła konieczne jest poznanie stałej π≈3,14159 26535..., która stanowi stosunek długości obwodu koła do jego średnicy.

Obwód okręgu bądź koła można obliczyć za pomocą następującego wzoru:

[1]

Zapis wyrażenia w formacie TeX-a:

L=2\cdot\pi\cdot R

Długość łuku z kolei można obliczyć z wzoru:

[2]

Zapis wyrażenia w formacie TeX-a:

L=\alpha\cdot R

Obwód wycinka okręgu:

[3]

Zapis wyrażenia w formacie TeX-a:

L=R\cdot\left(\alpha+2\right)

Obwód odcinka koła:

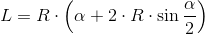[4]

Zapis wyrażenia w formacie TeX-a:

L=R\cdot\left(\alpha+2\cdot R\cdot\sin \frac{\alpha}{2}\right)

Pole powierzchni koła:

[5]

Zapis wyrażenia w formacie TeX-a:

P_{pow}=\pi \cdot R^2

Pole powierzchni wycinka koła:

[6]

Zapis wyrażenia w formacie TeX-a:

P_{pow}=\frac{\alpha}{2} \cdot R^2

Pole powierzchni odcinka koła:

[7]

Zapis wyrażenia w formacie TeX-a:

P_{pow}=R^2\cdot\left(\alpha-2\cdot\sin\frac{\alpha}{2}\cdot\cos\cfrac{\alpha}{2}\right)

Uwaga! We wszystkich wymienionych wzorach kąt α musi być wyrażony w radianach.

Matematyczny opis okręgu i koła

Każdy okrąg można opisać za pomocą następującego równania okręgu:

[8]

Zapis wyrażenia w formacie TeX-a:

(x-x_c)^2 + (y-y_c)^2= R^2

gdzie:

• x_c, y_c - współrzędne środka okręgu.

Parametryczna wersja opisu okręgu wygląda następująco:

[9]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} x = x_0 + r \cos \alpha\, \\ y = y_0 + r \sin \alpha\, \end{cases}

gdzie:

• α - kąt zawierający się od 0° do 360°.

Każde zaś koło można opisać następującą nierównością:

[10]

Zapis wyrażenia w formacie TeX-a:

(x-x_c)^2 + (y-y_c)^2leq R^2