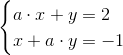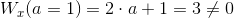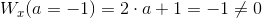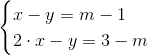Stronę tą wyświetlono już: 58160 razy

Wprowadzenie

Parametr jest to liczba, która należy do zbioru liczb rzeczywistych i ma wpływ na to, czy rozpatrywany układ równań liniowych ma: jedno rozwiązanie; nieskończenie wiele rozwiązań lub nie ma ich wcale.

Dany układ równań ma:

• jedno rozwiązanie, gdy współczynnik główny W ≠ 0;
• nieskończenie wiele rozwiązań, gdy współczynnik główny W = 0 i współczynniki W_x oraz W_y = 0;
• nie ma rozwiązań (jest sprzeczny), gdy wyznacznik główny W = 0 i ( współczynnik W_x ≠ 0 lub współczynnik W_y ≠ 0)

Wyżej wymienione współczynniki związane są z wzorami Cramera oraz z obliczaniem wyznacznika z macierzy kwadratowej, co opisane szczegółowo zostało na stronie Matematyka → Macierze → Wyznacznik macierzy.

Przykład rozwiązywania układów równań liniowych z parametrem

Przykład układu równań z parametrem a, dla którego należy określić dla jakich wartości tegoż parametru a układ ten jest:

• sprzeczny;
• ma nieskończenie wiele rozwiązań;
• ma jedno rozwiązanie.

A oto i upragniony układ równań z parametrem:

[1]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} a\cdot x+y=2 \\ x + a\cdot y = -1 \end{cases}

Obliczanie wyznacznika głównego:

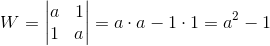[2]

Zapis wyrażenia w formacie TeX-a:

W=\begin{vmatrix}a & 1\\ 1 & a \end{vmatrix}=a\cdot a- 1 \cdot 1 = a^2-1

Obliczanie wyznacznika dla zmiennej x:

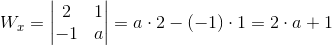[3]

Zapis wyrażenia w formacie TeX-a:

W_x=\begin{vmatrix}2 & 1\\ -1 & a \end{vmatrix}=a\cdot 2- (-1) \cdot 1 = 2\cdot a+1

Obliczanie wyznacznika dla zmiennej y:

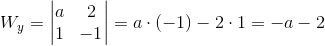[4]

Zapis wyrażenia w formacie TeX-a:

W_y=\begin{vmatrix}a & 2\\ 1 & -1 \end{vmatrix}=a\cdot (-1)- 2 \cdot 1 = -a-2

Teraz trzeba odpowiedzieć na pytanie: dla jakich wartości współczynnika a wyznacznik główny W ≠ 0? A oto i odpowiedź:

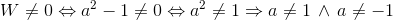[5]

Zapis wyrażenia w formacie TeX-a:

W\neq 0 \Leftrightarrow a^2-1\neq 0\Leftrightarrow a^2\neq 1\Rightarrow a\neq 1\,\wedge\,a\neq -1

Z powyższego wynika niezbicie, że rozpatrywany układ równań ma jedno rozwiązanie, gdy parametr a nie jest równy 1 lub -1. To rozwiązanie będzie miało następującą postać:

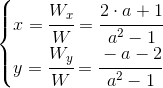[6]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} x=\cfrac{W_x}{W}=\cfrac{2\cdot a+1}{a^2-1} \\ y=\cfrac{W_y}{W}=\cfrac{-a-2}{a^2-1} \end{cases}

Pozostało jeszcze sprawdzenie, czy gdy współczynnik główny W jest równy 0, to któryś z współczynników W_x lub W_y jest różny od 0. Jeżeli tak, to układ nie ma rozwiązań, a jeżeli nie to ma ich nieskończenie wiele.

Sprawdzenie wartości współczynnika W_x dla a = 1 i a = -1:

[7]

Zapis wyrażenia w formacie TeX-a:

W_x(a=1) = 2\cdot a + 1 = 3 \neq 0

i dla a = -1:

[8]

Zapis wyrażenia w formacie TeX-a:

W_x(a=-1) = 2\cdot a + 1 = -1 \neq 0

Z powyższych jakże zaawansowanych obliczeń wynika niezbicie, że układ równań jest sprzeczny tak dla a = -1 jak i dla a = 1.

Zadania do samodzielnego rozwiązania:

Rozwiązać układy liniowych równań z parametrem:

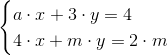[9]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} a\cdot x+3\cdot y=4 \\ 4\cdot x + m\cdot y = 2\cdot m \end{cases}

[10]

Zapis wyrażenia w formacie TeX-a:

\begin{cases} x- y=m-1 \\ 2\cdot x - y = 3-m \end{cases}