Wyznacznik macierzy
Stronę tą wyświetlono już: 19855 razy
Obliczanie wyznacznika macierzy 1×1 oraz 2×2.
Obliczenie wyznacznika macierzy A jest możliwe jedynie gdy owa macierz jest macierzą kwadratową. Wyznacznikiem macierzy 1×1 jest jej jedyny argument, natomiast dla macierzy o wymiarze 2×2 wyznacznik można obliczyć korzystając z następującego wzoru:
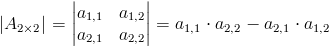 | [1] |
Zapis wyrażenia w formacie TeX-a:
Obliczanie wyznacznika macierzy 3×3 za pomocą reguły Sarrusa:
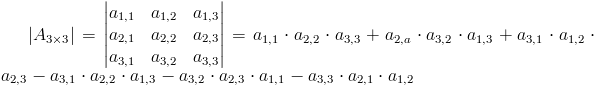 | [2] |
Zapis wyrażenia w formacie TeX-a:
Obliczanie wyznacznika macierzy kwadratowej wymiaru n>0 metodą Laplace'a
Ogólna postać wzoru na wyznacznik macierzy kwadratowej A o dowolnych wymiarach przyjmuje następującą postać:
gdzie:
- |Ai,k| - wyznacznik macierzy powstałej ze skreślenia i-tego wiersza i k-tej kolumny macierzy A (zwany też minorem macierzy A).
Wzór [3] umożliwia obliczenie wyznacznika macierzy A względem i-tego wiersza tejże macierzy. Podobny wzór można rozpisać dla i-tej kolumny:
gdzie:
- |Ak,i| - wyznacznik macierzy powstałej ze skreślenia k-tego wiersza i i-tej kolumny macierzy A (zwany też minorem macierzy A).
Właściwości macierzy zerowej
Istnieją przypadki, gdy jesteśmy w stanie stwierdzić z całą pewnością, że dana macierz jest macierzą zerową. Tak więc wyznacznik macierzy jest równy zero, gdy argumenty dowolnej kolumny lub wiersza macierzy są równe zero.
Przykład
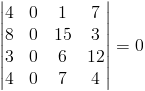
Wyznacznik macierzy jest równy zero, gdy dowolne dwa wiersze lub dwie kolumny są liniową kombinacją, to znaczy że jeżeli dla danych dwóch wierszy wi, wj gdzie i≠j istnieje taka liczba k, która spełnia następującą równość:
Podobny warunek należy zapisać dla kolumn danej macierzy prostokątnej:
Z powyższych zależności wynika, że jeżeli powtórzą się takie same wartości w dwóch dowolnych kolumnach o różnych indeksach lub dwóch dowolnych wierszach to wyznacznik macierzy jest równy zero.
Przykład:
Wyznacznik następującej macierz jest równy zero:
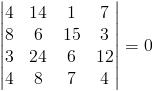
ponieważ druga i czwarta kolumna są liniowo zależne co wynika z zastosowania równości [6]:
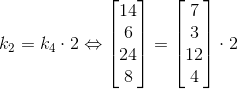
Teraz nieco trudniejszy do wykrycia przypadek, a więc w sytuacji gdy mamy trzy dowolne kolumny k, j i m, takie że k≠j i k≠m i j≠m. Jeżeli więc dla owych kolumn jest spełniona następująca zależność:
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_1908.gif) | [7] |
Zapis wyrażenia w formacie TeX-a:
W zależności [7] oczywiście a oraz b są dowolnymi liczbami rzeczywistymi. A wiec gdy zależność [7] zachodzi w danej macierzy, to takowa macierz jest macierzą o zerowym wyznaczniku. Prosty przykład macierzy 3×3:
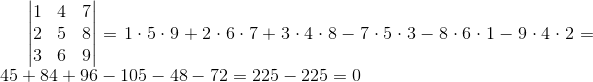
Powyższa macierz spełnia warunek [7] dla wierszy i jej wyznacznik jest zerowy co oznacza niezbicie, że zasada ta obowiązuje również dla trzech dowolnych wierszy macierzy.
Operacje na macierzach, które nie wpływają na zmianę ich wyznacznika
Drodzy Czytelnicy, istnieją pewne operacje, które nie wpływają na zmianę wyznacznika macierzy i o tych operacjach będę tutaj bliżej opowiadał.
Dodawanie do i-tego wiersza j-tego wiersza, takiego że i≠j.
Przykład:
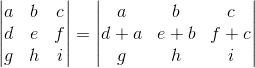
Dodawanie do i-tego wiersza j-tego wiersza przemnożonego przez skalar k, gdzie k≠0 oraz i≠j.
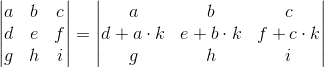
Kombinacje liniowe kilku wierszy, czyli dla przykładu dodanie do wiersza w3 wiersza w1 pomnożonego przez skalar k1 oraz wiersza w2 pomnożonego przez skalar k2.
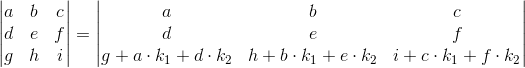
Operacje na macierzach, które powodują zmianę wyznacznika macierzy:
Jeżeli i-ty oraz j-ty wiersz macierzy zamieni się miejscami, to znak wyznacznika takiej macierzy zmieni się na przeciwny do macierzy pierwotnej. Założenie: i≠j. To samo dotyczy zamiany i-tej kolumny z j-tą kolumną.
Przykład:

Pomnożenie dowolnego jednego wiersza lub kolumny przez skalar k≠0 powoduje, że wyznacznik powstałej w ten sposób macierzy pomnożony przez odwrotność skalara k jest równy wyznacznikowi macierzy pierwotnej.
Przykład:
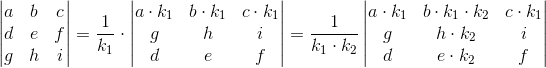
Wyznacznik macierzy diagonalnych
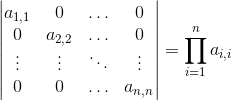
Macierz diagonalna to taka macierz, w której jedynie elementy na głównej przekątnej macierzy, na które składają się elementy ai,i, gdzie i jest równe od 1 do stopnia macierzy n są różne od zera. Innymi słowy macierz diagonalna ogólnie wygląda następująco:
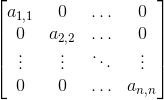
Wyznacznik takiej macierzy jest bardzo łatwy do policzenia, gdyż jest on równy iloczynowi elementów leżących na głównej przekątnej. Ogólny więc wzór na wyznacznik macierzy diagonalnej będzie wyglądał następująco:
Szczególną postacią macierzy diagonalnej jest macierz jednostkowa I. której wszystkie elementy na przekątnej głównej są równe 1. Również warto napomknąć, że jeżeli chociaż jeden element przekątnej macierzy diagonalnej jest równy zeru, to oczywiście wyznacznik takiej macierzy jest równy 0.
Wyznacznik macierzy trójkątnej górnej i trójkątnej dolnej
Jak się okazuje, również wyznacznik macierzy trójkątnej dolnej jak i macierzy trójkątnej górnej jest równy iloczynowi wszystkich elementów znajdujących się na głównej przekątnej macierzy. Macierz trójkątna to taka macierz, której wszystkie elementy nad (macierz trójkątna dolna) lub pod (macierz trójkątna górna) główną przekątną macierzy są równe 0.
Przykład macierzy trójkątnej dolnej:

Przykład macierzy trójkątnej górnej:

Wzór na wyznacznik macierzy trójkątnej górnej:
Wzór na wyznacznik macierzy trójkątnej dolnej:
Szybkie obliczanie wyznacznika macierzy
Wykorzystując w perfidny sposób wiadomości o tym, w jakich sytuacjach wyznacznik macierzy ulega zmianie i jakie te zmiany są a także znając metodę eliminacji Gaussa możemy w dość szybki sposób obliczyć wyznacznik macierzy. O samej metodzie eliminacji Gaussa nie będę się tutaj rozpisywał, albowiem dość dokładnie opisałem ją w dziale Matematyka → Macierze → Rozwiązywanie układów równań metodą eliminacji Gaussa, rozwiążę jednak przykład macierzy 5×5.
Dana jest więc macierz:

Trzeba zamienić metodą eliminacji Gaussa powyższą macierz do postaci macierzy trójkątnej górnej. Ponieważ pierwszy wiersz i pierwsza kolumna zawiera 1 to mogę już wyzerować pierwszą kolumnę znajdującą się pod elementem macierzy a1,1. W tym celu od danego wiersza odejmuję wiersz pierwszy pomnożony przez pierwszą wartość tego wiersza, czyli :
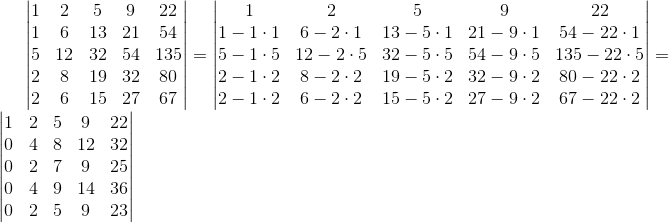
Do tej pory działania na macierzy zawierały się w zakresie takich, które nie wpływają na zmianę wyznacznika, teraz musimy podzielić wiersz drugi przez element a2,2 a więc zgodnie z wcześniej omawianymi zasadami aby utrzymać wartość wyznacznika pierwotnej macierzy trzeba wyznacznik przekształconej macierzy pomnożyć przez element a2,2.
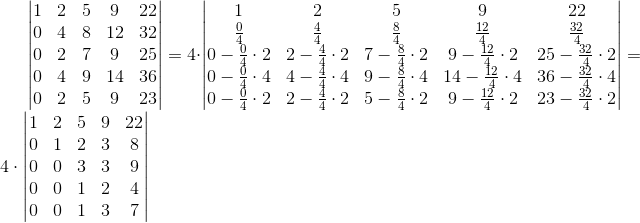
Jak widać powyżej nie rozdrabniałem się i od razu wyzerowałem elementy pod przekątną główną macierzy.
Teraz, tak jak uprzednio trzeba wiersz trzeci podzielić przez trzy i zredukować do zera elementy pod nim stojące.
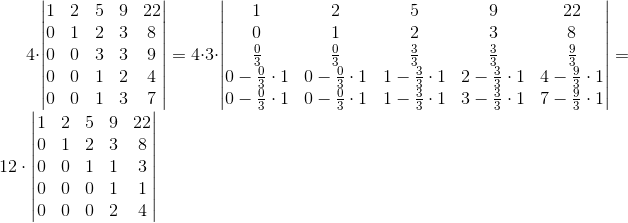
Ponieważ tak szczęśliwie się składa, że element a4,4=1, więc tym razem tylko zredukować trzeba do zera elementy znajdujące się pod nim, co też z najdzikszą rozkoszą czynię poniżej:

Jak widać na przekątnej pozostała już ostatnia wartość różna od 1, wystarczy teraz pomnożyć tą wartość przez współczynnik stojący przed wyznacznikiem ostatniej macierzy aby uzyskać wyznacznik macierzy pierwotnej, a więc:
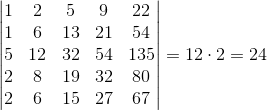
Przykład obliczania wyznacznika macierzy metodą Laplace'a
Obliczenia wyznacznika macierzy o wymiarach mniejszych niż 4×4 można wykonać korzystając w prosty sposób z wzorów [1], [2], jednakże dla lepszego zrozumienia wzoru [3] rozwiążę tutaj jeden przykład wyznacznika macierzy o rozmiarach 4×4.
Dane:
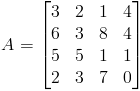
Rozwiązanie:
Obrałem ostatni wiersz macierzy A, ponieważ występuje w nim 0, które nieco upraszcza obliczenia.
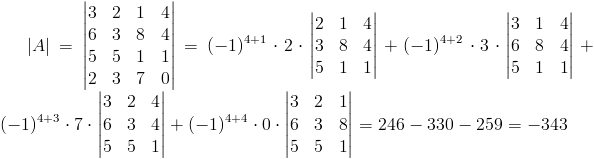
Wyznacznik macierzy ma spore zastosowanie w rozwiązywaniu układów równań liniowych, a wszystko to dzięki wzorom Cramera, w których olbrzymią rolę odgrywa umiejętność obliczania wyznacznika macierzy. Ogólny wzór wyznaczający i-tą niewiadomą ma następującą postać:
gdzie:
- Wxi - wyznacznik macierzy utworzonej z współczynników stojących przy niewiadomych za wyjątkiem kolumny, której odpowiada niewiadoma xi a za którą podstawić należy wartości wyrazów wolnych;
- Wg - wyznacznik główny macierzy utworzonej z współczynników stojących przy niewiadomych.
Warto napomknąć, że gdy Wg=0, układ równań nie da się rozwiązać, innymi słowy co najmniej jedno z równań jest kombinacją liniową drugiego.
Równanie [11] warto rozpatrzyć w kontekście następującego ogólnego układu równań:
gdzie:
- ai,j - współczynniki równania stojące przy niewiadomych;
- xi - niewiadome;
- wi - wyrazy wolne układu równań.
Wyznacznik główny dla układu równań [12] składa się z wyrazów współczynników stojących przy niewiadomych:
Wyznacznik Wxi dla i=1 będzie wyglądał następująco:
Przykład
Rozwiązać metodą wyznaczników układ równań z zadania 66 z działu Mechanika techniczna:Wytrzymałość materiałów:Konstrukcje prętowe statycznie niewyznaczalne.
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_341.gif) | [15] |
Zapis wyrażenia w formacie TeX-a:
Rozwiązanie:
Na podstawie układu równań [12] należy zapisać macierz główną Mg:
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_1158.gif) | [16] |
Zapis wyrażenia w formacie TeX-a:
Wektor wyrazów wolnych Ww:
Wyznacznik główny Wg macierzy głównej Mg:
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_1160.gif) | [18] |
Zapis wyrażenia w formacie TeX-a:
Wyznacznik macierzy utworzonej dla niewiadomej S1:
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_1161.gif) | [19] |
Zapis wyrażenia w formacie TeX-a:
Wyznacznik macierzy utworzonej dla niewiadomej S2:
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_1162.gif) | [20] |
Zapis wyrażenia w formacie TeX-a:
Wyznacznik macierzy utworzonej dla niewiadomej S3:
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_1163.gif) | [21] |
Zapis wyrażenia w formacie TeX-a:
Wyznacznik macierzy utworzonej dla niewiadomej S4:
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_1164.gif) | [22] |
Zapis wyrażenia w formacie TeX-a:
Zgodnie z wzorem [11] można wyznaczyć wartości niewiadomych:
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_1165.gif) | [23] |
Zapis wyrażenia w formacie TeX-a:

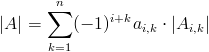
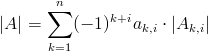
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_1148.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1149.gif)


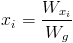
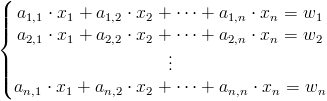
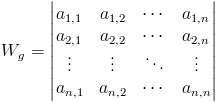

![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_1159.gif)