Hipocykloidy
Stronę tą wyświetlono już: 5129 razy
Definicja i rodzaje hipocykloid
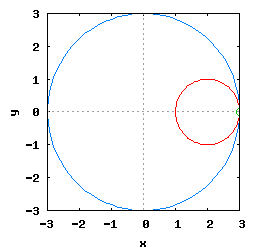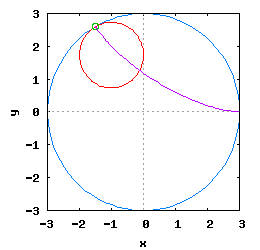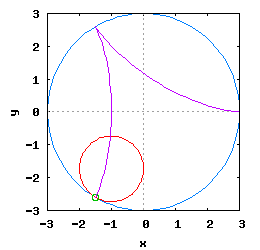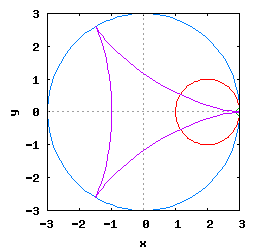
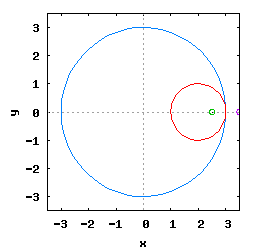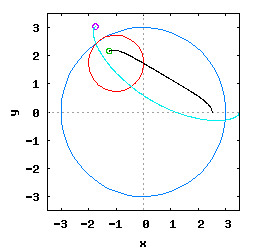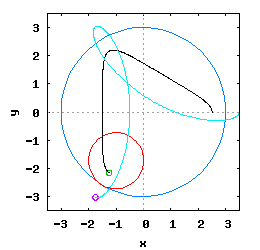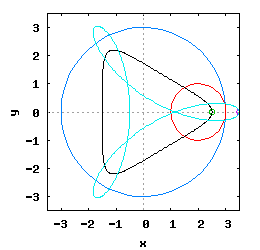
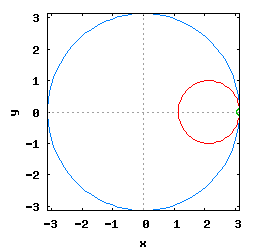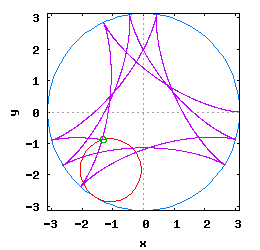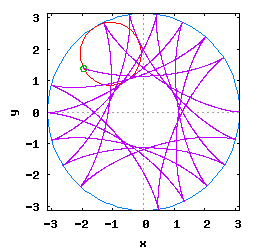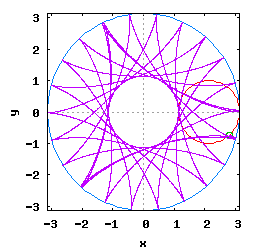
Hipocykloida to krzywa, jaką kreśli punkt umieszczony na obwodzie okręgu toczącego się po wewnętrznej stronie drugiego okręgu.
Hipocykloidę opisują trzy podstawowe parametry, którymi są:
- promień okręgu, po którym odbywa się toczenie Rw;
- promień okręgu toczącego się Ro;
- promień rysowania Rr
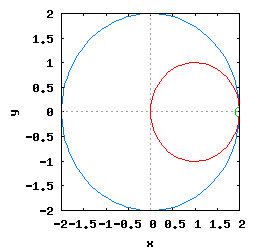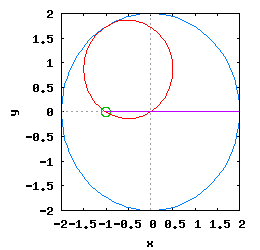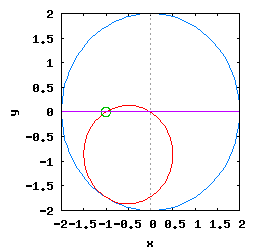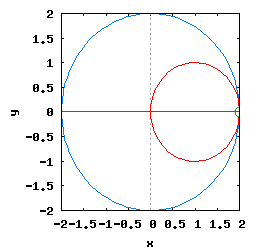
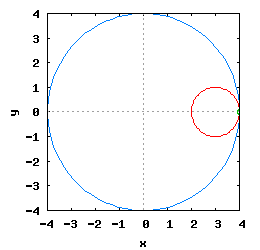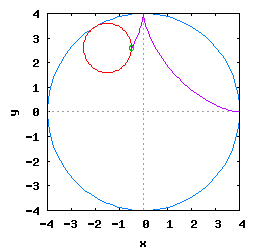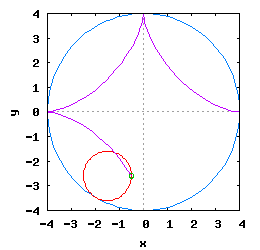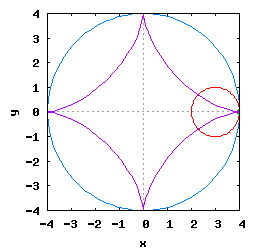
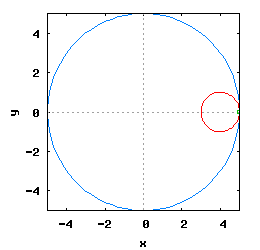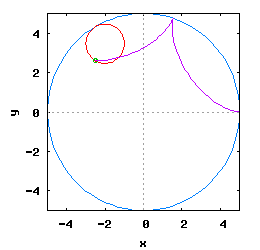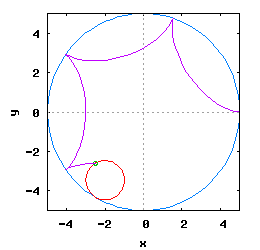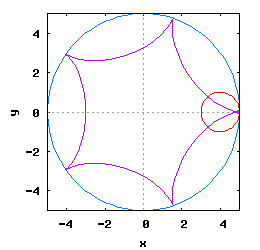
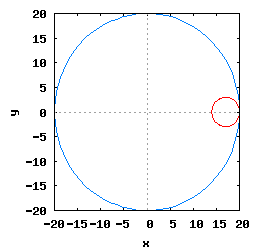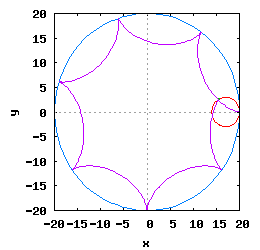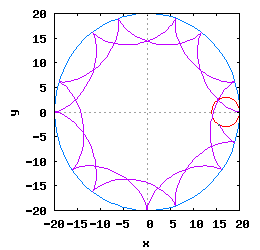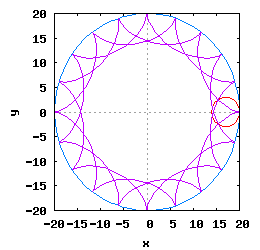
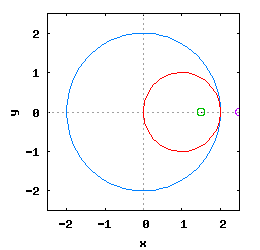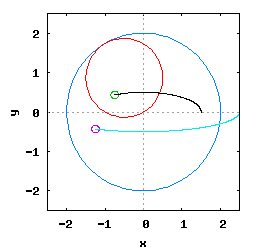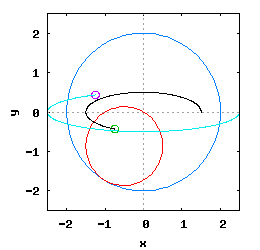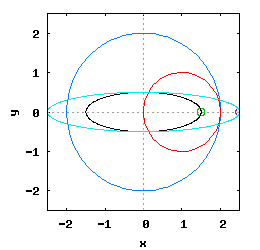
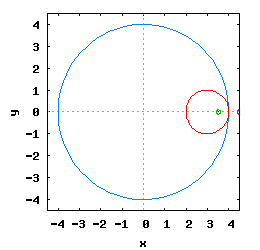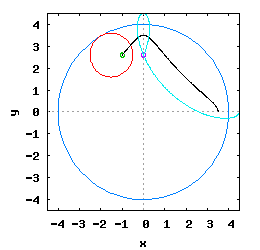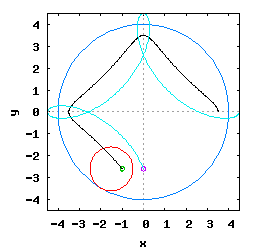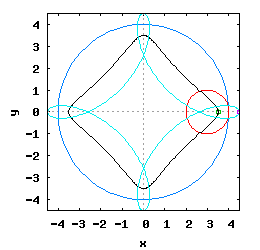
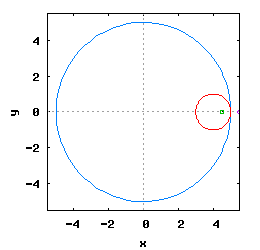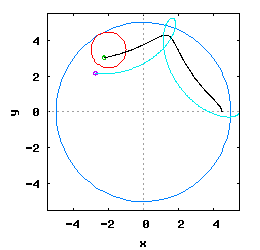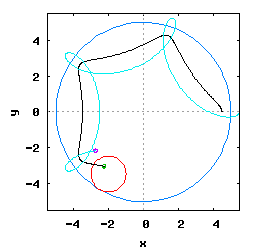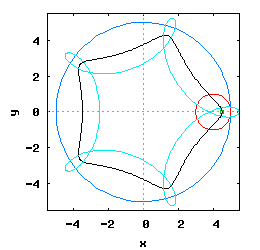
Gdy stosunek promienia Ro do promienia Rw jest ułamkiem zwykłym oraz jego odwrotność jest liczbą całkowitą, wtedy taka hipocykloida ma charakter cykliczny, którego okres wynosi 2·π radiana. Na poniższej rysunko-animacji pokazane zostały cztery takie hipocykloidy.
- a) o stosunku Ro do Rw równym 1/2;
- b) o stosunku Ro do Rw równym 1 / 3 ;
- c) o stosunku Ro do Rw równym 1 / 4 ;
- d) o stosunku Ro do Rw równym 1 / 5 .
Klatki do powyższych animacji zostały wykonane w programie wxMaxima, natomiast poskładane zostały w programie Gimp
Hipocykloidy, których stosunek promienia Ro do Rw jest ułamkiem zwykłym ale jego odwrotność nie jest liczbą całkowitą mają okres większy niż jeden pełny obrót. Przykład takiej hipocykloidy można zobaczyć na poniższym rysunku.
Klatki do powyższych animacji zostały wykonane w programie wxMaxima za pomocą następującego kodu:
W powyżej rozpatrywanych przypadkach promień rysowania Rr jest równy promieniowi okręgu Ro, istnieje jednak możliwość, aby promienie te się od siebie różniły, takie przypadki pokazują poniższe animacje.
- a) o stosunku Ro do Rw równym 1/2 o promieniach rysowania 1,5·Ro i 0,5·Ro;
- b) o stosunku Ro do Rw równym 1 / 3 o promieniach rysowania 1,5·Ro i 0,5·Ro;
- c) o stosunku Ro do Rw równym 1 / 4 o promieniach rysowania 1,5·Ro i 0,5·Ro;
- d) o stosunku Ro do Rw równym 1 / 5 o promieniach rysowania 1,5·Ro i 0,5·Ro.
Klatki do powyższych animacji zostały wykonane w programie wxMaxima, natomiast poskładane zostały w programie Gimp
Gdy stosunek promienia Ro do promienia Rw nie da się wyrazić za pomocą ułamka zwykłego, wtedy krzywa nie zamyka się cyklicznie a jedynie może zbliżać się i oddalać od swoich krawędzi tworząc bliskie zamknięciu się przejście. Przypadek ten obrazuje poniższa animacja.
Klatki do powyższych animacji zostały wykonane w programie wxMaxima za pomocą następującego kodu:
Uwaga! Czas wykonywania klatek animacji za pomocą powyższego kodu jest dość długi.
Parametryczny opis hipocykloidy
Dla hipocykloidy podstawowej, czyli takiej, dla której promienie Ro i Rr są sobie równe opis parametryczny przyjmuje następującą postać:
W przypadku, gdy Ro≠Rr wtedy równania parametryczne przyjmują postać następującą:
Zastosowanie i miejsca występowania epicykloid
W przekładniach planetarnych punkty na obwodzie kół pośredniczących w przenoszeniu momentu obrotowego z obwiedniowego koła zębatego na koło centralne poruszają się po hipocykloidach w układzie związanym z obwiedniową zębatką. Takie koła stosowane są w niektórych rowerach miejskich, gdzie w piaście wbudowany jest system przekładni planetarnych, jednakże tam to koło centralne pozostaje w bezruchu a obwiedniowe kręci się wraz z satelitarnymi kołami pośredniczącymi.
Hipocykloida z rysunku 1 a) z powodzeniem może zostać wykorzystana w niecnym planie zamiany ruchu posuwisto zwrotnego na obrotowy i na odwrót. Innymi słowy z tego można by zrobić albo silnik spalinowy, albo pompę np. wodną.
Rodzina hipocykloid, których dwaj przedstawiciele pokazani zostali na rysunku 3 a) umożliwiają kreślenie elips.

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2116.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2117.gif)
