Obliczenia układów dynamicznych metodą prac przygotowawczych
Stronę tą wyświetlono już: 4060 razy
Obliczyć przyspieszenie ac krążka toczącego się bez poślizgu po poziomej płaszczyźnie połączonego za pośrednictwem nieważkiego i nierozciągliwego cięgna z krążkiem, do którego przyłożony został moment obrotowy M będący jedynym czynnikiem wywołujący ruch układu.
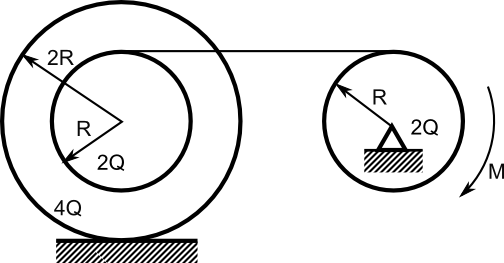
Dane:
![R[m]; Q[N]; M[Nm]](rownania/w_579.gif)
Rozwiązanie:
Na rysunku 1 zaznaczone zostały jedynie podstawowe informacje, bez oznaczenia wektorów liniowego przyspieszenia a, przyspieszeń kątowych ε a także przesunięć prac przygotowawczych układu niezbędnych do ułożenia równania d'Alamberte'a. Innymi słowy trzeba zrobić nowy rysunek z wszystkimi potrzebnymi oznaczeniami (co też i z najdzikszą rozkoszą czynię poniżej).
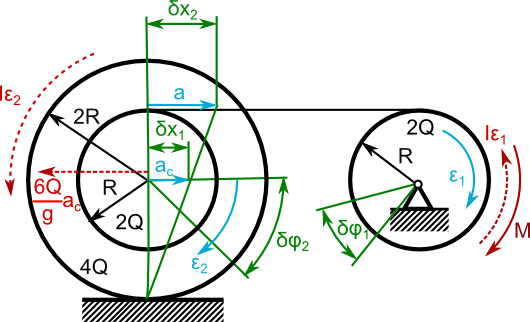
Zgodnie z wcześniej omawianą teorią, suma iloczynów założonego przesunięcia i sił bezwładności FB oraz iloczynu sił sprawczych i założonego dla nich przesunięcia musi równać się zeru. Ważne jest, żeby pamiętać o kierunku bo wektory przeciwne mają przeciwny znak.
Równanie d'Alamberte'a dla rozpatrywanego układu będzie więc wyglądało następująco:
Po uporządkowaniu powyższego równania otrzymuję:
W powyższym równaniu jest całkiem sporo niewiadomych, do których należą między innymi przemieszczenia. Nie ma jednak powodów do paniki, albowiem pozbyć się ich można korzystając z wzajemnych zależności przemieszczeniowych. Ułożę więc zależność wszystkich przemieszczeń od przemieszczenia δx1 a dlaczego do δx1? Odpowiedź brzmi: bo taki mam kaprys.
Zależność przemieszczenia δφ2 od przemieszczenia δx1:
Zależność przemieszczenia δx2 od przemieszczenia δx1:
Zależność przemieszczenia δφ1 od przemieszczenia δx1:
Podstawić pozostało już tylko do równania [2] zależności przemieszczeniowe [3], [4] oraz [5] otrzymując:
Równanie [6] podzielić obustronnie przez δx1 i uprościć otrzymując tym samym:
Pozostało już tylko opisanie zależności kinetycznych, w celu pozbycia się kolejnych niewiadomych.
Zależność kinetyczne ε2 od ac:
Zależność kinetyczne a2 od ac:
Zależność kinetyczne ε1 od ac:
Podstawienie do równania [7] zależności [8], [9] i [10]:
Po podzieleniu przekształceniu i uproszczeniu otrzymuje się upragnioną wartość ac.
Obliczyć przyśpieszenie ac krążka o masie m zawieszonego na nieważkim i nierozciągliwym cięgnie.

Dane:
![r[m];m[kg]](rownania/w_588.gif)
Rozwiązanie:
Przed przystąpieniem do rozwiązania zadania, uzupełnić należy najpierw oznaczenia na rysunku 3 tak jak to zostało wykonane na rysunku 4.
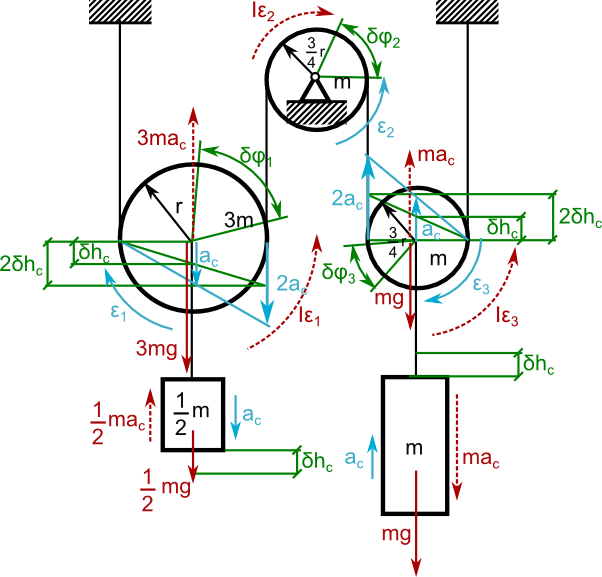
Jak widać, na rysunku 4 naniesione już zostały podstawowe zależności przemieszczeń liniowych w zależności od hc oraz liniowych przyspieszeń w zależności od ac co ułatwi rozpisanie równania d'Alamberte'a:
Po uproszczeniu otrzymuje się następującą postać równania [13]:
Zależności przemieszczeń:
Podstawienie do równania [14] zależności [15], [16] i [17]:
Uproszczenie wyrażenia [18]:
Zależności kinetyczne:
Podstawiając zależności [20], [21] i [22] do równania [19] z jednoczesnym uproszczeniem i przekształceniem otrzymuje się szukaną wartość ac:
Obliczyć przyśpieszenie ac krążka o ciężarze 4Q zawieszonego na nieważkim i nierozciągliwym cięgnie.

Dane:
![r[m];Q[N]](rownania/w_604.gif)
Rozwiązanie:
Tradycyjnie od uzupełnienia rysunku zacząć trzeba.
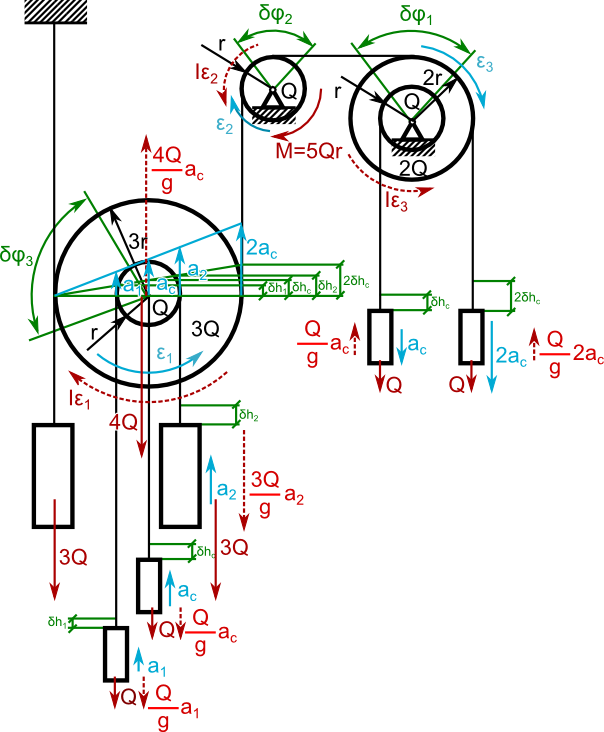
Równanie d'Alamberte'a rozpisać trzeba:
Upraszczając równanie [24] odrobinę otrzymuje się następującą jego postać:
Zależności przemieszczeń:
Po podstawieniu do zależności [25] wyrażeń [26] do [30] i uproszczeniu otrzymuje się następujące równanie:
Zależności kinetyczne:
Po podstawieniu do równania [31] zależności [32] do [36], uproszczeniu i przekształceniu otrzymuje się wartość przyspieszenia ac:
Obliczyć przyśpieszenie a ciężarka o masie 2m położonego na płaskiej poziomej płaszczyźnie. W układzie należy pominąć tarcie ciężarków o podłoże oraz masę cięgna.

Dane:
![R[m];m[kg]](rownania/w_627.gif) α=30°
α=30°
Rozwiązanie:
Naniesienie dodatkowych oznaczeń na rysunku 8.
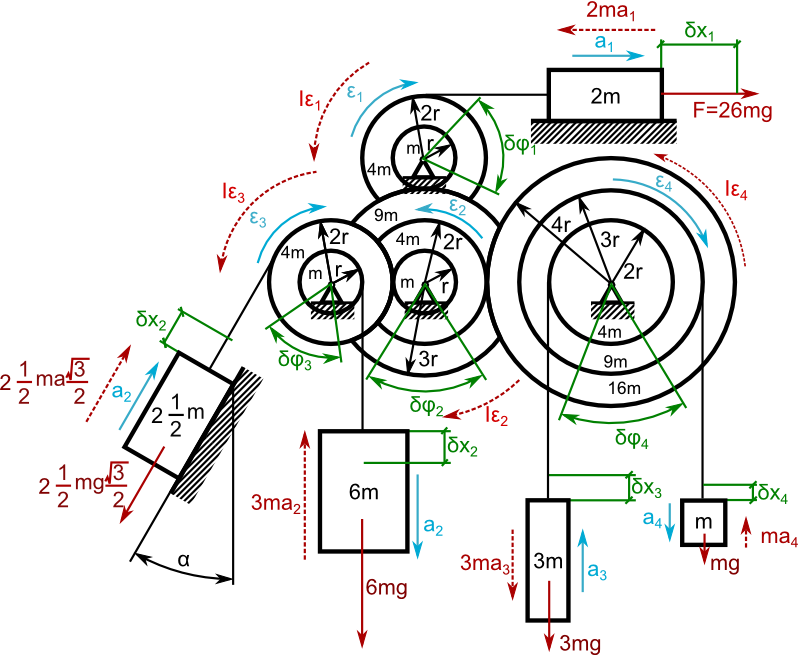
Po raz kolejny trzeba rozpisać równanie d'Alamberte'a:
Po uproszczeniu równania [38] otrzymuje się taką oto jego postać:
Prawda, że ładne równanko wyszło? Zaraz się uprości, gdy tylko rozpisze się przemieszczeń zależności:
Jak uprzednio tak i teraz podstawionko zrobić trzeba, czyli do równania [39] podstawić należy zależności od [40] do [46], co też i z najdzikszą rozkoszą czynię równocześnie upraszczając:
Jakże piękne równanie [46] zawiera kilka niewiadomych, do których pozbycia się należy wykorzystać w perfidny sposób zależności kinetyczne:
I ponownie choć tym razem do równania [47] trzeba zrobić małe podstawienie zależności od [48] do [54], a następnie uprościć je i przekształcić uzyskując wartość przyspieszenia a.
Zadanie 5 - ostatnie starcie
Obliczyć przyśpieszenie a krążka toczącego się bez poślizgu po równi pochyłej.

Dane:
![R[m];m[kg]](rownania/w_627.gif)
Rozwiązanie:
Uzupełnienie oznaczeń.
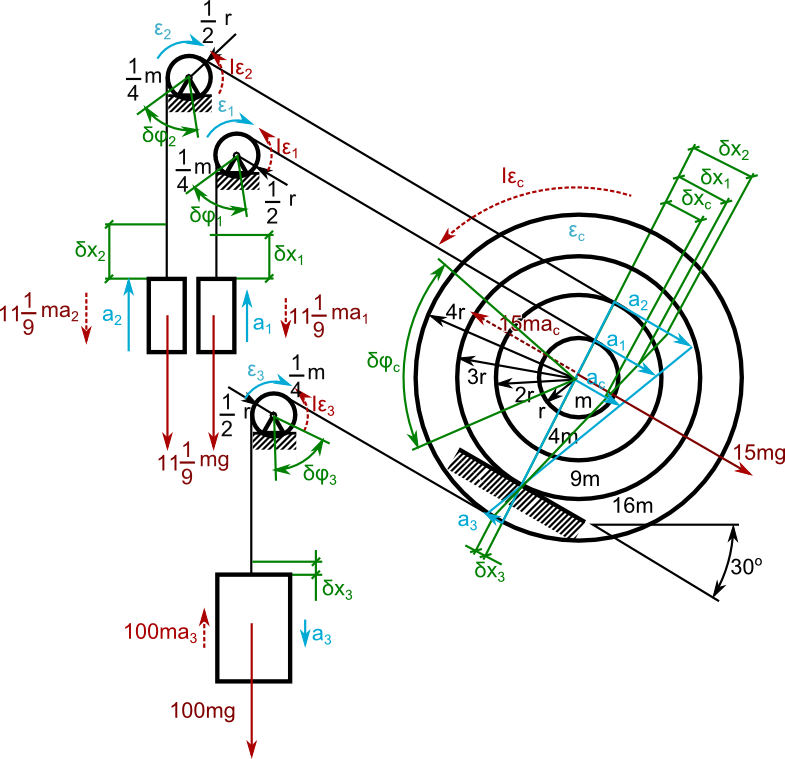
Równanie d'Alamberte'a:
Powyższe równanie, choć piękne to jednak warto conieco uprościć:
Spokojnie, równanie powyższe się uprości, gdy rozpisze się przemieszczeń zależności:
Podstawiając do równania [57] zależności [58] do [64] i upraszczając otrzymuje się następujące równanie:
Piękne powyższe równanie jest, zgodzicie chyba się? Nie? Niektórych ludzi trudno zadowolić, ale dobra to się zmieni gdy rozpisane i podstawione zostaną zależności kinetyczne:
Najwyższy czas do równania [65] podstawić zależności [68] do [72] jednocześnie uproszczając i przekształcając dzięki czemu uzyskuje się wartość przyspieszenia ac.

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2245.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2246.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2247.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2248.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2249.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2250.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2251.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2252.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2253.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2254.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2255.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_2256.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_2257.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_2258.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_2259.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_2260.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_2261.gif)
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_2262.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_2263.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_2264.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_2265.gif)
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_2266.gif)
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_2267.gif)
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_2268.gif)
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_2269.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_2270.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_2271.gif)
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_2272.gif)
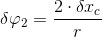
![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_2274.gif)
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_2275.gif)
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_2276.gif)
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_2277.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_2278.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_2279.gif)
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_2280.gif)
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_2281.gif)
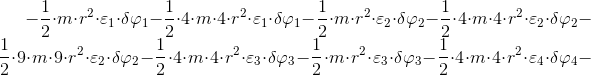
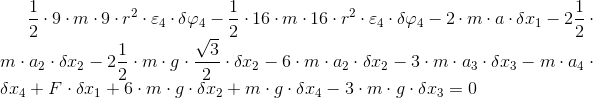
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_2284.gif)
![Równanie [40]](https://obliczeniowo.com.pl/rownania/w_2285.gif)
![Równanie [41]](https://obliczeniowo.com.pl/rownania/w_2286.gif)
![Równanie [42]](https://obliczeniowo.com.pl/rownania/w_2287.gif)
![Równanie [43]](https://obliczeniowo.com.pl/rownania/w_2288.gif)
![Równanie [44]](https://obliczeniowo.com.pl/rownania/w_2289.gif)
![Równanie [45]](https://obliczeniowo.com.pl/rownania/w_2290.gif)
![Równanie [46]](https://obliczeniowo.com.pl/rownania/w_2291.gif)
![Równanie [47]](https://obliczeniowo.com.pl/rownania/w_2292.gif)
![Równanie [48]](https://obliczeniowo.com.pl/rownania/w_2293.gif)
![Równanie [49]](https://obliczeniowo.com.pl/rownania/w_2294.gif)
![Równanie [50]](https://obliczeniowo.com.pl/rownania/w_2295.gif)
![Równanie [51]](https://obliczeniowo.com.pl/rownania/w_2296.gif)
![Równanie [52]](https://obliczeniowo.com.pl/rownania/w_2297.gif)
![Równanie [53]](https://obliczeniowo.com.pl/rownania/w_2298.gif)
![Równanie [54]](https://obliczeniowo.com.pl/rownania/w_2299.gif)
![Równanie [55]](https://obliczeniowo.com.pl/rownania/w_2300.gif)
![Równanie [56]](https://obliczeniowo.com.pl/rownania/w_2301.gif)
![Równanie [57]](https://obliczeniowo.com.pl/rownania/w_2302.gif)
![Równanie [58]](https://obliczeniowo.com.pl/rownania/w_2303.gif)
![Równanie [59]](https://obliczeniowo.com.pl/rownania/w_2304.gif)
![Równanie [60]](https://obliczeniowo.com.pl/rownania/w_2305.gif)
![Równanie [61]](https://obliczeniowo.com.pl/rownania/w_2306.gif)
![Równanie [62]](https://obliczeniowo.com.pl/rownania/w_2307.gif)
![Równanie [63]](https://obliczeniowo.com.pl/rownania/w_2308.gif)
![Równanie [64]](https://obliczeniowo.com.pl/rownania/w_2309.gif)
![Równanie [65]](https://obliczeniowo.com.pl/rownania/w_2310.gif)
![Równanie [66]](https://obliczeniowo.com.pl/rownania/w_2311.gif)
![Równanie [67]](https://obliczeniowo.com.pl/rownania/w_2312.gif)
![Równanie [68]](https://obliczeniowo.com.pl/rownania/w_2313.gif)
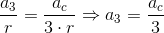
![Równanie [70]](https://obliczeniowo.com.pl/rownania/w_2315.gif)
![Równanie [71]](https://obliczeniowo.com.pl/rownania/w_2316.gif)
![Równanie [72]](https://obliczeniowo.com.pl/rownania/w_2317.gif)
![Równanie [73]](https://obliczeniowo.com.pl/rownania/w_2318.gif)