Zasada równowagi pracy i energii
Stronę tą wyświetlono już: 14319 razy
W sytuacjach, gdy energia kinetyczna układu mechanicznego jest zależna od pracy, jaką na tym układzie wykonują siły zewnętrzne można zastosować zasadę równoważności energii kinetycznej układu i pracy na nim wykonanej co zapisuje się w następujący sposób:
Powyższe równanie mówi, że suma wszystkich prac L wykonanych na układzie jest równa sumie energii E wszystkich elementów rozpatrywanego układu. Dzięki poprawnemu zrozumieniu tego zapisu, można rozwiązywać zadania z strony Mechanika techniczna → Dynamika → Obliczenie przyspieszeń układów ciał metodą Newtona.
By możliwe było zastosowanie równania [1] w praktyce, trzeba przypomnieć sobie nieco wzorów z fizyki na poziomie szkoły średniej. Na pierwszy rzut ognia niech pójdzie wzór na energię kinetyczną obiektu materialnego:
A teraz wzór na energię kinetyczną (bezwładność) krążka obracającego się wzdłuż osi symetrii:
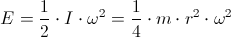 | [3] |
Zapis wyrażenia w formacie TeX-a:
To już są wszystkie wzory dotyczące energii, jakie będą potrzebne do rozwiązywania wcześniej wspomnianych typów zadań, teraz czas dobrać się do wzorów na pracę L. Najpierw jednak odpowiedzmy sobie, jakie czynniki mogą wykonać pracę (a tym samym nadać układowi energię kinetyczną)? Są to z pewnością: siła P, masa m lub ciężar (siła ciężkości) i moment siły M.
Praca jaką wykona przyłożona do układu siła jest równa:
gdzie s to droga przebyta przez ciało pod wpływem działającej siły P.
Ciężar z kolei wykonuje pracę daną wzorem na energię potencjalną Ep:
gdzie:
- m to masa danego ciała;
- g - przyspieszenie ziemskie 9,80665 [m/s2];
- h - przemieszczenie w polu grawitacyjnym (gdy równe zero, to praca L równa jest zero).
Ważne jest, aby pamiętać, że praca w polu grawitacyjnym ma charakter zachowawczy. Oznacza to tylko tyle, że jeżeli początkowe i końcowe położenie obiektu w polu grawitacyjnym będą takie same, to praca będzie równa zero. Dla lepszego poglądu sytuacji wystarczy spojrzeć na poniższą ilustrację.

W przypadku rowerzysty praca L2-3 wykonana przez grawitację jest przyjęta jako ujemna, ponieważ rowerzysta nie wkłada żadnego wysiłku na jej wykonanie, natomiast odwrotnie ma się rzecz, gdy rowerzysta wjeżdża pod górkę, tutaj już nie ma tak różowo i trzeba zasuwać samemu i dlatego praca L4-5 rośnie. Można jednak przyjąć odwrotny scenariusz, to znaczy, przyjąć że praca L2-3 wykonana przez grawitację jest dodatnia, a ta wykonana przez rowerzystę L4-5 ujemna.
Praca wykonana przez moment siły M jest równa iloczynowi tegoż momentu siły M i przemieszczenia kątowego φ wyrażonego w radianach.


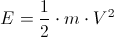
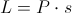

![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1808.gif)