Prawdopodobieństwo
Stronę tą wyświetlono już: 3309 razy
Rachunek prawdopodobieństwa jest działem matematyki zajmujący się badaniem prawdopodobieństwa z zakresu doświadczeń losowych.
Klasyczna definicja prawdopodobieństwa
Jeżeli zbiór Ω składa się z n zdarzeń elementarnych i zdarzeniu losowemu A⊂Ω sprzyja k zdarzeń elementarnych o jednakowym prawdopodobieństwie wystąpienia, to liczbę równą ilorazowi zdarzeń sprzyjających zajściu zdarzenia A do liczby wszystkich zdarzeń elementarnych Ω nazywa się prawdopodobieństwem zajścia zdarzenia A, co opisuje poniższy wzór:
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2459.gif) | [1] |
Zapis wyrażenia w formacie TeX-a:
P(A)=\frac{\overline{\overline{A}}}{\overline{\overline{B}}}=\frac{k}{n}
Przykład
Rzucamy jeden raz kostką do gry. Jakie jest prawdopodobieństwo tego, że wypadło więcej niż 2 oczka?
Rozwiązanie:
Jest to doświadczenie jednoetapowe, a więc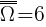 
bo Ω={1; 2; 3; 4; 5; 6}.
A - zdarzenie, w którym wyrzucona liczba oczek jest większa od dwóch.
W tym przypadku A={3; 4; 5; 6}, 
Podstawiając do wzoru [1] obliczamy prawdopodobieństwo zdarzenia A
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2460.gif)
Prawdopodobieństwo wyrzucenia większej liczby oczek niż 2 wynosi w przybliżeniu 66,6%.
Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray
Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha
Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett
Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew
Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner
Tytuł:
Sprawdziany Matematyka Klasa 3
Autor:
Iwona Kowalska, Beata Guzowska
Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan
Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol
Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek
Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota