Całki nieoznaczone
Stronę tą wyświetlono już: 8890 razy
Całka nieoznaczona to zbiór wszystkich funkcji pierwotnych f określonych w przedziale X oznaczanych w następujący sposób:
Powyższy zapis należy czytać w następujący sposób: całka f od x dx
gdzie:
- f(x) - funkcja podcałkowa;
- x - zmienna całkowania;
- dx - różniczka zmiennej całkowania;
- f(x) dx - wyrażenie podcałkowe.
Całkowanie jest odwrotnym działaniem w stosunku do pochodnej, z czego wynika następująca równość:
Funkcja F(x) jest funkcją pierwotną funkcji f(x) wtedy i tylko wtedy gdy spełniona jest następująca równość:
Istnieje następująca zależność pomiędzy całkowaniem funkcji f(x) a funkcją pierwotną F(x):
gdzie:
- c - stała całkowania

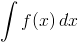
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1327.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1328.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1329.gif)