Przyspieszenie styczne, normalne i binormalne
Stronę tą wyświetlono już: 23822 razy
Definicje, interpretacja geometryczna i przykładowe obliczenia
Tak się nieszczęśliwie składa, że wektor całkowity a(t) nie jest jednocześnie wektorem stycznym do funkcji toru lotu, nie jest on również wektorem prostopadłym do funkcji toru lotu a te dwie wielkości fizyczne okazują się najbardziej przydatne.
Ktoś mógłby zadać jednak pytanie: a co z wektorem V(t), dlaczego dla niego nie liczymy stycznych i normalnych? Szczęście w nieszczęściu polega na tym, że nasz wektor V(t) jest pochodną funkcji przemieszczenia r(t) a więc wektor V(t) musi być styczny do r(t) (czego powiedzieć nie można w przypadku wektora a(t).
Dla lepszego zrozumienia powagi sytuacji zerknijmy łaskawym okiem na rysunek 1, który w zasadzie jest animacją. Na owym rysunku - animacji widoczne są: v(t) - zaznaczony na zielono (może być niewidoczny bo przykryty przez wektor przyspieszenia stycznego); a(t) - zaznaczony na ciemno niebieski kolor; ast - zaznaczony na kolor magenta; an - zaznaczony na kolor jasno niebieski. Wszystkie te wektory zostały obliczone dla danej wartości t, której wartość zmienia się od 0,05 [s] do 1 [s] z krokiem co 0,05 [s].
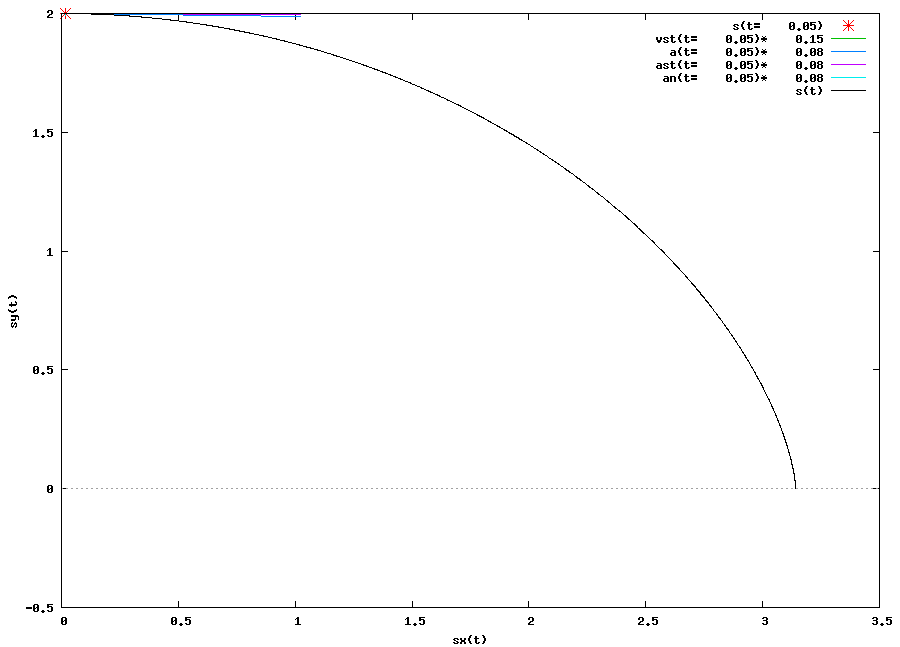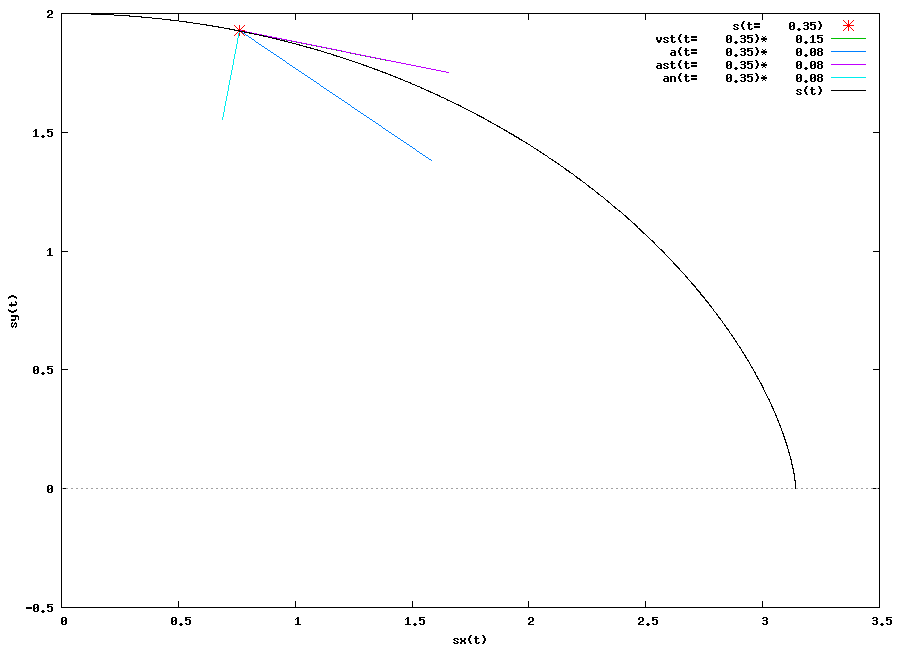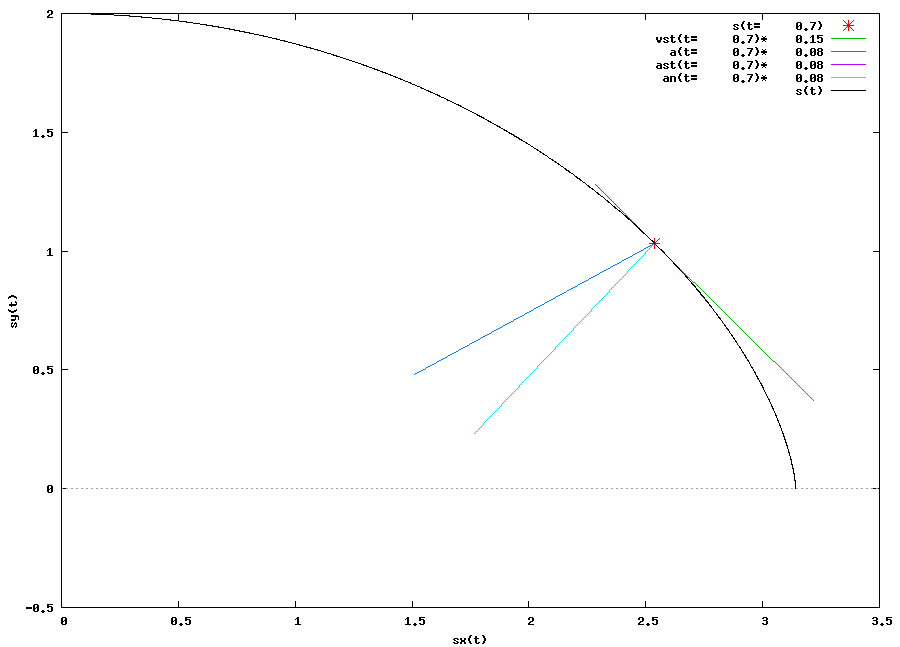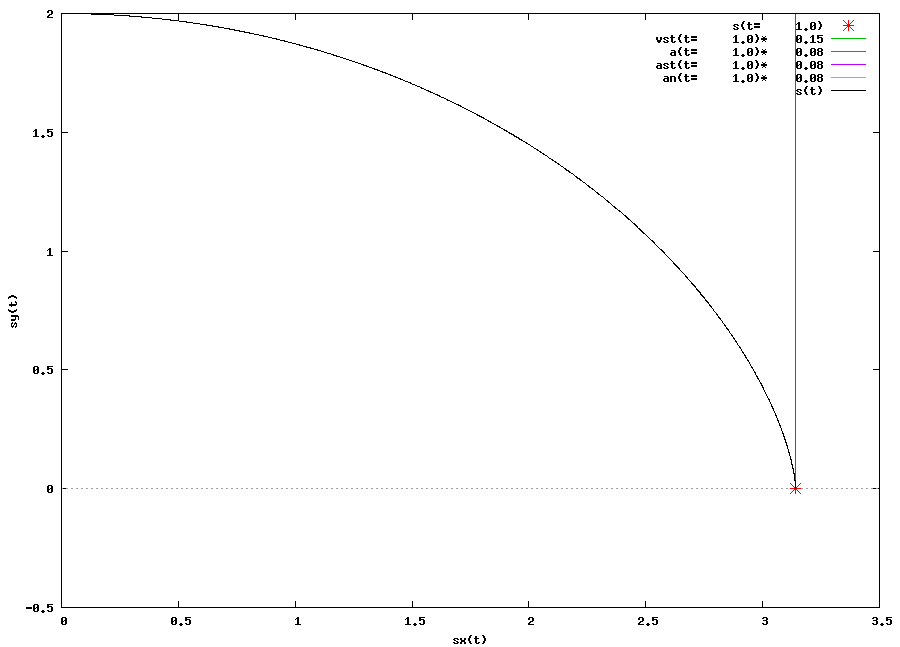
Wykres wygenerowany w programie wxMaxima
Nie będę ukrywał, że animacja z rysunku 1 dotyczy bezpośrednio zadania 3 z strony Fizyka → Kinematyka → Funkcje zależności położenia w różnych układach odniesienia oraz zadania 2 z strony Fizyka → Kinematyka → Funkcje zależności przemieszczenia, prędkości i przyspieszenia w różnych układach odniesienia.
Skoro już wiadomo, że wektor całkowity przyspieszenia a(t) nie jest styczny do funkcji toru ruchu r(t) to trzeba coś z tym zrobić. I tutaj przychodzi na pomoc układ współrzędnych związanych bezpośrednio z funkcją trajektorii ruchu r(t). Układ ten definiują trzy wektory: wektor styczny T do funkcji r(t) w danym punkcie; wektor normalny N oraz wektor binormalny B, którego wartość jest różna od zera jedynie wtedy, gdy wektor przyspieszenia całkowitego nie leży w płaszczyźnie wektorów T i N. Wektory N, T oraz B są wektorami jednostkowymi i ortogonalnymi (prostopadłymi do siebie). Wektory te dla danego punktu danej funkcji r(t) tworzą trójścian Frenata jak na rysunku 2.
Wektor przyspieszenia stycznego w układzie wektorów podstawowych Frenata przyjmuje następującą postać:
Załóżmy, że wektor przyspieszenia binormalnego aB jest równy zero a co za tym idzie wektor całkowitego przyspieszenia a(t) leży w płaszczyźnie wektorów: stycznego T i normalnego N, w takim bowiem przypadku można obliczyć wektor przyspieszenia stycznego ast·T z następującego wzoru:
oraz wektor przyspieszenia normalnego an·N z zależności:
gdzie:
δ - promień funkcji w danym punkcie.
Zwróćmy swe oczęta w kierunku wcześniej wspomnianego zadania i spróbujmy obliczyć wartość przyspieszenia stycznego ast dla czasu t=3/4 [s].
Funkcja prędkości całkowitej po czasie:
Funkcje Vx(t) i Vy(t) zostały już policzone w zadaniu 2 są to wzory [16] i [17]:
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2503.gif) | [5] |
Zapis wyrażenia w formacie TeX-a:
Nie muszę chyba przekonywać, że dość kłopotliwa w obliczaniu jest to pochodna i dlatego za promień R przyjmuję wartość 1 i rozwiązanie tej pochodnej obliczone w programie wxMaxima wrzucam poniżej.
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1910.gif) | [6] |
Zapis wyrażenia w formacie TeX-a:
Po podstawieniu i przeliczeniu dla ast(t=3/4 [s]) przyjmuje wartość równą -9.193920464282291 [m/s2].
Wyznaczmy jeszcze wektor styczny T wykorzystując w przebiegły sposób wzór [3] z działu Matematyka → Wektory → Iloczyn wektorowy przez liczbę. Jak wiadomo już nam wektor prędkości V(t) jest wektorem stycznym do funkcji toru ruchu, a więc wystarczy go podzielić przez jego długość aby otrzymać poszukiwany wektor styczny T:
Wyznaczmy nasz wektor V(t=3/4 [s]):
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2505.gif) | [8] |
Zapis wyrażenia w formacie TeX-a:
Długość wektora już policzona będzie więc wynosiła 5.979015843045633, co po podstawieniu do wzoru [7] wraz ze wzorem [8] daje wektor styczny T(t=3/4 [s]):
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2506.gif) | [9] |
Zapis wyrażenia w formacie TeX-a:
Teraz już spokojnie mogę obliczyć wektor ast(t=3/4 [s]) mnożąc wektor T przez skalar ast(t=3/4 [s]):
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2507.gif) | [10] |
Zapis wyrażenia w formacie TeX-a:
Wektor przyspieszenia a(t=3/4 [s]) będzie potrzebny aby wyznaczyć wektor przyspieszenia normalnego an (wzory potrzebne do wyliczenia wypadkowych wektora a zostały wyprowadzone w zadaniu 2):
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2508.gif) | [11] |
Zapis wyrażenia w formacie TeX-a:
Przyspieszenie normalne an(t=3/4 [s]) jest więc równe:
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_2509.gif) | [12] |
Zapis wyrażenia w formacie TeX-a:
Teraz pragnę pokazać sposób, jak obliczyć wektor przyspieszenia stycznego ast(t) bez liczenia pochodnej funkcji prędkości całkowitej V(t). Wystarczy bowiem obliczyć rzut prostopadły wektora przyspieszenia całkowitego a(t=3/4 [s]) na wektor prędkości v(t=3/4 [s]) korzystając z wzoru [6] z działu Matematyka → Wektory → Iloczyn skalarny w następujący sposób:
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_2510.gif) | [13] |
Zapis wyrażenia w formacie TeX-a:
gdzie za t podstawiono oczywiście 3/4 [s].
Na rysunku 3 można a nawet trzeba zobaczyć jak te nasze wektory będą wyglądały na wykresie. Oczywiście wektory te zostały przeskalowane proporcjonalnie, tak aby mieściły się na wykresie.
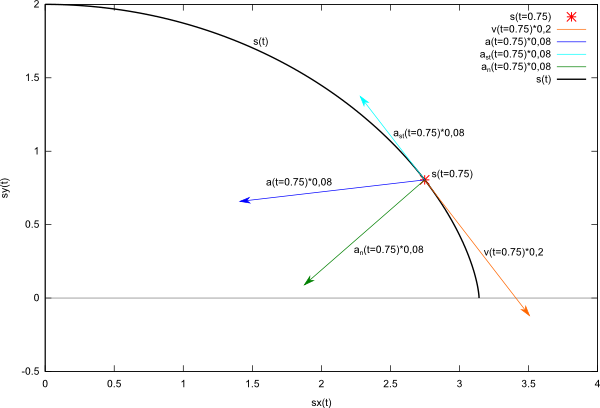
Wykres wygenerowany do pliku svg w programie wxMaxima
Wykres edytowany w programie Inskcape
Właściwości wektorów przyspieszenia stycznego ast i normalnego an
Na wstępie muszę napisać o ciekawym przypadku wektora prędkości całkowitej V(t), dla której nie jest możliwe wyznaczenie za pomocą wzorów [2] i [7] wektora przyspieszenia stycznego ast. Gdy wektor prędkości całkowitej V(t) dla danego t jest wektorem zerowym to przyspieszenie styczne ast(t) jest równe przyspieszeniu całkowitemu a(t) a co za tym idzie przyspieszenie normalne an jest wtedy równe zero. Co ciekawe, w takim momencie t przyspieszenie całkowite a(t) uzyskuje maksimum globalne lub maksimum lokalne.
Rozważmy teraz przypadek, gdy wektor przyspieszenia stycznego ast(t) jest wektorem zerowym. W takim przypadku wektor przyspieszenia normalnego an(t) przyjmuje wartość maksimum globalnego lub maksimum lokalnego.
Przyspieszenie styczne ast(t) - jest to przyspieszenie jakie działa w danym momencie t na punkt materialny w układzie lokalnym związanym z funkcją trajektorii ruchu s(t). Nie ulega więc wątpliwości fakt, że gdy wartość przyspieszenia stycznego ast(t)>0 to nasz punkt przyspiesza po krzywej funkcji s(t), gdy przyspieszenie styczne ast=0 prędkość punktu V(t)=const (jest stała) no i ostatni przypadek, gdy przyspieszenie styczne ast<0 wtedy prędkość maleje.
Przyspieszenie normalne an - jest to przyspieszenie, które określa kierunek zakrzywienia trajektorii lotu. Gdy więc wartość przyspieszenia normalnego an=0, to albo funkcja s(t) zmienia kierunek zakrzywienia toru ruchu albo funkcja ta nie jest zakrzywiona.
Zadania
Zadanie 1
Most o rozpiętości L=200 [m] wznosi się na wysokość h=10[m]. Sprawdzić, czy Fiat 126p jest w stanie rozpędzić się do takiej prędkości, pod wpływem której oderwie się on od powierzchni mostu, widząc że łuk mostu opisuje funkcja kwadratowa.
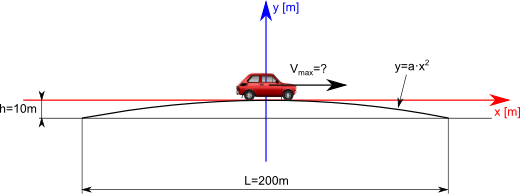
Dla funkcji mostu y=a·x2 trzeba wyznaczyć współczynnik a, co też z najdzikszą rozkoszą czynię wiedząc, że dla x=100 [m], f(x=100)=-10 [m]. W związku z czym parametr a=-0,001. Z tego wynika niezbicie, że nasza funkcja opisująca trajektorię ruchu ma następującą postać:
Pomyślmy przez chwilę logicznie i zastanówmy się, jakie warunki muszą zaistnieć, aby nasz Fiat 126p oderwał się od ziemi? Odpowiedź brzmi: przyspieszenie normalne an, które jest też miarą przyspieszenia odśrodkowego o przeciwnym zwrocie musi być większe od przyspieszenia ziemskiego g.
Dla x=0 [m] (strzałka ugięcia) trzeba obliczyć przyspieszenie normalne an(x=0 [m]) korzystając w tym celu z wzoru [3], w liczniku którego znajduje się szukana prędkość Vmax. W mianowniku z kolei znajduje się promień krzywizny funkcji, który obliczymy korzystając z wzorów [5] i [2] z strony Fizyka → Kinematyka → Krzywizna i promień funkcji.
Obliczmy najpierw krzywiznę κ funkcji y=0,001·x2 z wzoru [2]:
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_2512.gif) | [15] |
Zapis wyrażenia w formacie TeX-a:
Teraz zgodnie z wzorem [5] z strony Fizyka → Kinematyka → Krzywizna i promień funkcji obliczyć należy promień δ funkcji y(x=0):
Zgodnie z wzorem [3] wartość przyspieszenia normalnego an(x=0) jest równa:
Gdy przyspieszenie styczne an jest równe g to samochód oderwie się od ziemi, dlatego też szukamy takiego Vmax, dla którego spełniona jest nierówność:
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_2515.gif) | [18] |
Zapis wyrażenia w formacie TeX-a:
Wniosek jest jeden, Fiat 126p nie jest w stanie oderwać się od ziemi, no chyba że ktoś zamontuje na jego dachu silnik odrzutowy.
Zadanie 2
Obliczyć dla zadania 6 z strony Fizyka → Kinematyka → Funkcje zależności przemieszczenia, prędkości i przyspieszenia w różnych układach odniesienia przyspieszenie styczne ast i normalne an.
W trakcie rozwiązywania zadania 6 doszliśmy do niezbitych wniosków, że:
- ruch odbywa się w układzie współrzędnych walcowych;
- składowa z wektora przyspieszenia jest równa zero;
- promień r jest równy parametrowi a funkcji trajektorii ruchu
Udowodnić można również, że wartość wektora prędkości jest stała i wynosi:
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_2516.gif) | [19] |
Zapis wyrażenia w formacie TeX-a:
Ponieważ wartość wektora prędkości V(t) jest stała (co wynika z równania [19]), więc przyspieszenie styczne ast jest równe zero.
Mówiłem już wcześniej, że gdy wektor przyspieszenie stycznego ast(t) jest wektorem zerowym to wektor przyspieszenia normalnego an(t) jest równy wektorowi przyspieszenia całkowitego a(t). Z tego wniosek, że nasz wektor przyspieszenia opisuje następujące równanie:
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_2517.gif) | [20] |
Zapis wyrażenia w formacie TeX-a:
Na koniec tego zadania, wyznaczę wartość wektora przyspieszenia normalnego an, tylko po to, by udowodnić, że jest to wektor o stałej wartości, lecz o zmiennym kierunku:
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_2518.gif) | [21] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 3
Pociąg wyrusza ze stacji kolejowej jadąc po łuku o promieniu 4 [km]. Dane jest równanie drogi po czasie s(t):
Obliczyć przyspieszenie styczne ast i normalne an pociągu w chwili, gdy ten osiągnie prędkość V(t)=180 [km/h].
Koniecznie trzeba wyznaczyć wzór na prędkość chwilową po czasie, a będzie on przyjmował następującą postać (pochodna drogi po czasie):
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_2520.gif) | [23] |
Zapis wyrażenia w formacie TeX-a:
Ponieważ V(t)=180 [km/h] a szukane jest t, równanie [23] przekształcam do następującej postaci:
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_2521.gif) | [24] |
Zapis wyrażenia w formacie TeX-a:
Druga pochodna równania drogi po czasie s(t) jest niczym innym jak wzorem na przyspieszenie styczne ast(t), a więc dla wyliczonego czasu t=500 [s] liczymy wartość drugiej pochodnej drogi po czasie:
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_2522.gif) | [25] |
Zapis wyrażenia w formacie TeX-a:
Przyspieszenie normalne w tym przypadku jest obliczyć bardzo prosto, albowiem wystarczy podstawić do wzoru [3] wartość prędkości V=180 [km/h] = 50 [m/s] i za promień δ=4 [km] = 4000 [m], by uzyskać upragnioną wartość przyspieszenia normalnego an, co też i z najdzikszą rozkoszą czynię:
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_2523.gif) | [26] |
Zapis wyrażenia w formacie TeX-a:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2499.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2500.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2501.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2502.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2504.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_2511.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_2513.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_2514.gif)
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_2519.gif)
