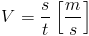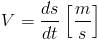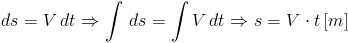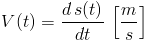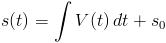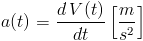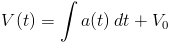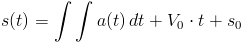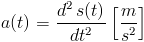Ruch, droga, czas

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 7686 razy

Ruch, jak już zresztą była o tym mowa, jest to zmiana położenia obiektu w zadanym przedziale czasu. Pytanie zagadka to jak opisać ruch? Zapewne wytycznymi ruchu jest prędkość, przyspieszenie oraz droga i położenie.

Prędkość najogólniej rzecz ujmując jest to stosunek przebytej drogi s do przedziału czasu Δt, w którym droga s została pokonana.

Wzór na prędkość [1]

Zapis wyrażenia w formacie TeX-a:

V=\frac{s}{t}\left[\frac{m}{s}\right]

Znając elementarne przemieszczenie ds w elementarnej jednostce czasu dt można zapisać następujące równanie różniczkowe:

Wzór na prędkość jako pochodną drogi s po czasie t [2]

Zapis wyrażenia w formacie TeX-a:

V=\frac{ds}{dt}\left[\frac{m}{s}\right]

Przekształcając wyrażenie [2] i całkując je obustronnie otrzymuje się wzór na drogę s w zależności od czasu t oraz prędkości V.

Wzór na drogę s w zależności od czasu dla ruchu jednostajnego [3]

Zapis wyrażenia w formacie TeX-a:

ds=V\,dt\Rightarrow \int\,ds=\int V\,dt\Rightarrow s=V\cdot t

Wzory [1], [2] oraz [3] opisują ruch jednostajny jednakże co z przypadkiem, w którym prędkość się zmienia i można ją wyrazić funkcją V(t), zaś przemieszczenie funkcją s(t)? W takim przypadku prędkość chwilowa jest równa pochodnej funkcji s(t) po czasie t.

Wzór ogólny opisujący zależność funkcji prędkośći V(t) od pochodnej funkcji drogi s(t) po czasie t [4]

Zapis wyrażenia w formacie TeX-a:

V(t)=\frac{d\,s(t)}{dt}\,\left[\frac{m}{s}\right]

Przekształcając powyższą równość podobnie jak w przypadku wzoru [3] uzyskany zostanie wzór na położenie s przemieszczającego się obiektu.

Ogólny wzór na funkcję drogi s(t) zależną od całki z funkcji prędkości V(t) [5]

Zapis wyrażenia w formacie TeX-a:

s(t)=\int V(t)\,dt+s_0

gdzie:

Kolejną bardzo ważną wielkością fizyczną jest przyspieszenie a, które wyraża stosunek różnicy prędkości V2-V1 do różnicy czasów t2-t1, w których zmiana prędkości się dokonała. Owe różnice zastępuje się dla uproszczenia zapisem ΔV oraz Δt.

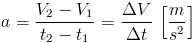Wzór na przyspieszenie a w ruchu jednostajnie zmiennym [6]

Zapis wyrażenia w formacie TeX-a:

a=\frac{V_2-V_1}{t_2-t_1}=\frac{\Delta V}{\Delta t}\,\left[\frac{m}{s^2}\right]

Najprościej rzecz ujmując przyspieszenie a jest to nic innego jak zmiana prędkości V w przedziale czasu Δt. Wyrażając prędkość wzorem V(t) i obierając elementarną zmianę owej prędkości dV(t) w elementarnym przedziale czasu dt można zapisać następującą równość:

Wzór zależności funkcji przyspieszenia a(t) od pochodnej funkcji prędkości V(t) [7]

Zapis wyrażenia w formacie TeX-a:

\a(t)=\frac{d\,V(t)}{dt}\left[\frac{m}{s^2}\right]

Przekształcając równość [7] otrzymuje się wzór na prędkość dla zadanej funkcji przyspieszenia a(t).

Wzór zależności funkcji V(t) od całki funkcji a(t) po czasie t [8]

Zapis wyrażenia w formacie TeX-a:

V(t)=\int a(t)\,dt+V_0

gdzie:

Podstawiając za V(t) do wzoru [5] wzór [8] otrzymuje się wzór na położenie s(t) obiektu w zależności od czasu t:

Zależność funkcji drogi s(t) od całki podwójnej z funkcji przyspieszenia a(t) po czasie t [9]

Zapis wyrażenia w formacie TeX-a:

s(t)=\int\int a(t)\,dt+V_0\cdot t+s_0

gdzie:

Z kolei podstawiając do wzoru [7] za V(t) wzór [4] uzyskuje się wzór na przyspieszenie a(t):

Wzór zależności funkcji przyspieszenia a(t) od drugiej pochodnej po funkcji drogi s(t) [10]

Zapis wyrażenia w formacie TeX-a:

a(t)=\frac{d^2\,s(t)}{dt^2}\left[\frac{m}{s^2}\right]

Przyspieszenie a(t) jest równe drugiej pochodnej położenia s(t) po czasie t.

Warto nadmienić, że omówione wielkości fizyczne takie jak przyspieszenie a, prędkość V oraz położenie s są wielkościami wektorowymi i jako takie mają wartość, kierunek i zwrot.