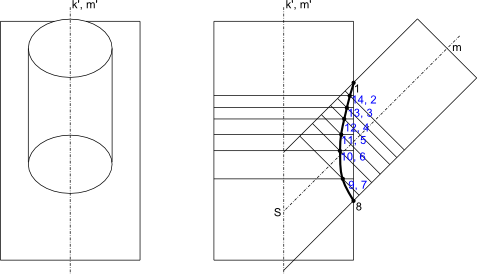Wyznaczanie krawędzi przenikania dwóch walców metodą sfer współśrodkowych
Stronę tą wyświetlono już: 26963 razy
Metoda sfer współśrodkowych ma pewne ograniczenia, takie że:
1) przenikające się bryły muszą być bryłami obrotowymi;
2) osie owych brył muszą się przecinać w jednym punkcie a tym samym wyznaczać jedną wspólną płaszczyznę;
3) rzutnia główna musi być ustawiona równolegle do płaszczyzny przechodzącej przez osie symetrii przenikających się brył obrotowych.
W przypadku dwóch walców mamy jasny wniosek, że punkt 1) jest spełniony. Natomiast na tej stronie będę rozpatrywał taki przypadek ustawienia osi symetrii walców i ułożenia płaszczyzny rzutowania tak, aby spełnione zostały pozostałe warunki.
Rozpatrzmy więc przypadek z rysunku 1, gdzie dane są dwa walce. I tu jedną uwagę napiszę, co prawda na rysunku narysowałem elipsy w jednym z rzutów, ale są one tak naprawdę narysowane tylko po to, aby uświadomić, że to są walce. Innymi słowy, nie interesuje nas kreślenie tutaj elips.
Przy wyznaczaniu punktów przenikania się naszych walców istotną rolę odgrywają osie symetrii k i m walców oraz punkt ich przecięcia S, ponieważ z tego właśnie punktu należy wykreślić serię łuków o średnicy mniejszej niż odległość pomiędzy punktami S i 1 a większej niż odległość pomiędzy punktami S i 8. Po utworzeniu takiej siatki, należy połączyć przecięcia danego łuku z walcem o osi symetrii k oraz z walcem o osi symetrii m. Przecięcia odpowiadających sobie otrzymanych w ten sposób linii wyznaczają szukane przez nas punkty przenikania się walców jak to zresztą pokazałem na rysunku 2.
Pozostało nam już tylko połączenie kolejnych punktów co też z najdzikszą rozkoszą pozwoliłem sobie uczynić na poniższym rysunku.
Wyznaczone zostały już punkty na prawym rzucie, czas zabrać się za wyznaczenie położenia punktów na lewym rzucie. Zanim jednak, to najpierw znajdźmy odległości tych punktów od osi symetrii na rzucie lewym, a uczynimy to poprzez wykreślenie na rzucie prawym półokręgu dla walca o osi symetrii k i zrzutowaniu nań punktów liniami równoległymi do osi symetrii k. Odległość od odcinka łączącego końce utworzonego półokręgu do punktu przecięcia się z nim odpowiadają odległościom poszczególnych punktów od osi symetrii k na rzucie lewym rysunku. Dzięki temu można a nawet trzeba znaleźć poszczególne punkty przenikania się naszych walców na rzucie lewym, co też i uczyniłem na poniższym rysunku.
Na koniec, oczyścić pozostało rysunek z zbędnych linii pomocniczych, pozostawiając tym samym tylko i wyłącznie to, co nas interesuje.