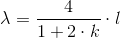Drgania struny jednostronnie podpartej
Stronę tą wyświetlono już: 2648 razy
Struną jednostronnie podpartą może być np. pręt zamocowany w ścianie, w który ktoś uderza wzbudzając w nim falę akustyczną. Długość fali, które można wzbudzić w takiej strunie opisuje następujący wzór:
gdzie:
- λ - długość fali akustycznej;
- l - długość struny;
- k - liczba naturalna (0, 1, 2, 3).
Obliczenie częstotliwości drgań takiej struny umożliwia następujący wzór:
gdzie:
- λ - długość fali akustycznej;
- l - długość struny;
- k - liczba naturalna (0, 1, 2, 3);
- V - prędkość dźwięku rozprzestrzeniającego się w materiale, z jakiego zrobiona została struna.
Powyższe wzory są prawdziwe, ponieważ struna jest z jednej strony podparta co wymusza powstawanie fal akustycznych, które w miejscu podparcia będą miały zerowe wychylenie drgań, zaś z drugiej strony pręt może się przemieszczać swobodnie, co z kolei wymusza aby fale kończyły się tam maksymalnym możliwym wychyleniem. Dla lepszego zrozumienia warto rzucić okiem na poniższą ilustrację.
Rys. 1
Struna jednostronnie podparta i przykładowe fale akustyczne, jakie mogą w niej powstawać: czerwona - fala o częstotliwości podstawowej; niebieska - fala o długości λ równej 4/3 długości struny l
Propozycje książek