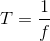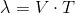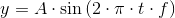Akustyka
Stronę tą wyświetlono już: 3579 razy
Akustyka to dział fizyki zajmujący się badaniem zjawisk związanych z powstawaniem, rozprzestrzenianiem i oddziaływaniem fal akustycznych. Zakres fal słyszalnych przez przeciętnego zjadacza chleba wynosi od około 16 [Hz] do 20 [kHz].
Fale akustyczne można podzielić pod względem ich częstotliwości na następujące podstawowe grupy:
- infradźwięki - poniżej 16 Hz;
- dźwięki słyszalne - od 16 Hz do 20 kHz - odbiera je większość ludzi;
- ultradźwięki - powyżej 20 kHz;
- hiperdźwięki - powyżej 1010 Hz.
Dźwięki słyszane przez nas na co dzień najczęściej są dźwiękami złożonymi, na które składa się kilka lub więcej różnych fal o podstawowych. Każda fala podstawowa może zostać opisana za pomocą następujących podstawowych właściwości:
- częstotliwość f - wyrażana w Hercach [Hz] jest to liczba drgań na jednostkę czasu. Ta wielkość fizyczna jest związana z okresem T fali akustycznej;
- okres T - opisuje czas wykonania jednego pełnego drgania fali akustycznej. Powiązanie okresu z częstotliwością fali f jest następujące:
- długość fali λ - jest związana ściśle z prędkością rozchodzenia się fali w danym ośrodku przy danej temperaturze a i niekiedy ciśnieniu oraz z okresem fali T. Jeżeli przez V oznaczyć prędkość fali akustycznej w danym ośrodku to długość fali λ da się obliczyć z następującego wzoru:
- amplituda A - jest to maksymalna zmiana ciśnienia ośrodka względem stanu normalnego
Przebieg zmiany ciśnienia ośrodka można zapisać za pomocą ogólnego wzoru następującej postaci:
gdzie:
- A - amplituda wychyleń ciśnienia;
- f - częstotliwość drgania;
- t - czas;
- y - zmiana ciśnienia w punkcie początkowym wywoływanej fali akustycznej
Możliwe jest również wyprowadzenie wzoru na ciśnienie powietrza w dowolnym punkcie oddalonym o x od jego źródła za pomocą następującego wzoru:
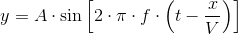 | [4] |
Zapis wyrażenia w formacie TeX-a:
Poniżej pokazany został przykładowy wykres funkcji zmiany ciśnienia ośrodka w centrum jego powstawania.