Wykresy momentów gnących i sił tnących w belekach statycznie niewyznaczalnych
Stronę tą wyświetlono już: 14121 razy
Rozwiązywanie belek statycznie niewyznaczalnych metodą energetyczną zgodnie z zasadą najmniejszej pracy. W celu wyznaczenia energii sprężystego odkształcenia belki konieczne jest zastosowanie równania Castigliano wyznaczającego strzałkę ugięcia belki pod wpływem sił odkształcających:
gdzie:
- fi - strzałka ugięcia belki
- dU - pochodna energii sprężystej
- dP - pochodna siły
Korzystając z równania [1] można napisać następujące równanie energii sprężystej dowolnej belki:
Wyznaczyć reakcje belki jednokrotnie statycznie niewyznaczalnej z rysunku 1.
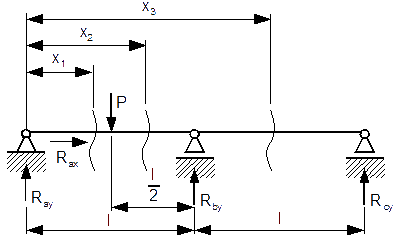
Dane:
![l=1[m]; P=1[kN]](rownania/w_433.gif)
Rozwiązanie:
Jak widać na załączonym rysunku, to już nie przelewki, to już jest prawdziwa belka statycznie niewyznaczalna są trzy podpory, możliwe jest ułożenie dwóch "pożytecznych" równań statycznych, i brakuje oczywiście jednego równania do pełni szczęścia. Zanim ułożę to równanie, najpierw stare dobre równania równowagi:
Ostatnie równanie wymaga rozpisania funkcji momentów gnących M(x) dla poszczególnych przedziałów, oraz pochodnych tej funkcji po reakcji obranej jako statycznie niewyznaczalna, która musi znajdować się na krańcu lewej lub prawej strony belki, ja obrałem jako statycznie niewyznaczalną reakcje Ray. Należy pamiętać również, że wszystkie niewiadome w równaniu, należy zastąpić ich zależnością od reakcji obranej jako statycznie niewyznaczalną.
Przedział 1
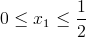
No to liczymy pierwszą część równania energii sprężystej belki:
Przedział 2
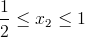
Przedział 3
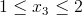
Teraz właśnie do równania M(x3) należy za reakcję Rby podstawić z równania [4] w następujący sposób:
Przyjmując, że belka jest wykonana z jednorodnego metalu oraz ma taki sam przekrój na całej długości, współczynnik znajdujący się przed całką z równania [2] można pominąć. Dla liczonej belki statycznie niewyznaczalnej należy zsumować wszystkie równania uzyskane dla poszczególnych przedziałów belki, i otrzymaną w ten sposób sumę przyrównać do zera.
Znając wartość reakcji Ray można obliczyć reakcję Rby:
Znając wartość reakcji Ray i Rby można obliczyć reakcję Rcy:
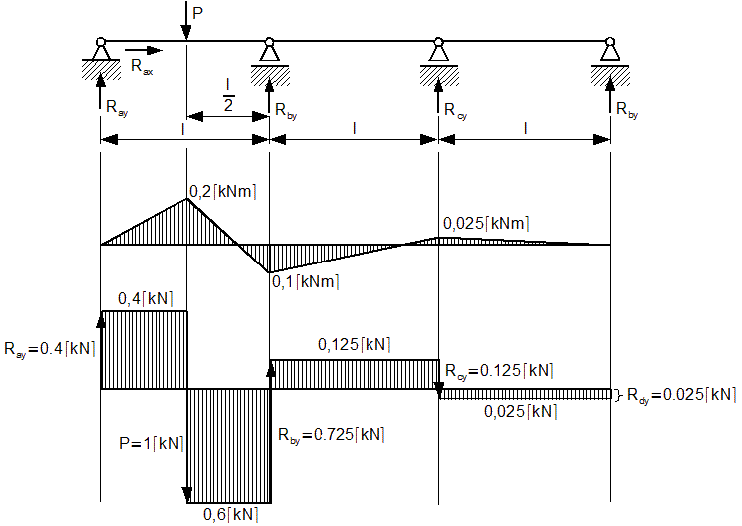
Pozostało obliczenie wartości po przedziałach dla wykresów momentów gnących i sił skręcających.
Przedział 1
Przedział 2
Przedział 3
Wykresy
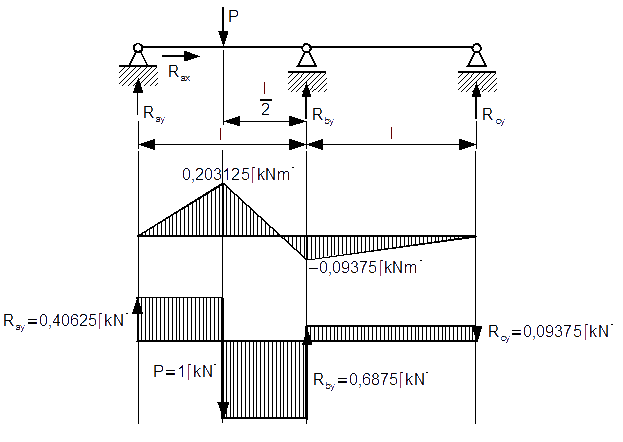
Wyznaczyć reakcje belki dwukrotnie statycznie niewyznaczalnej z rysunku 3.
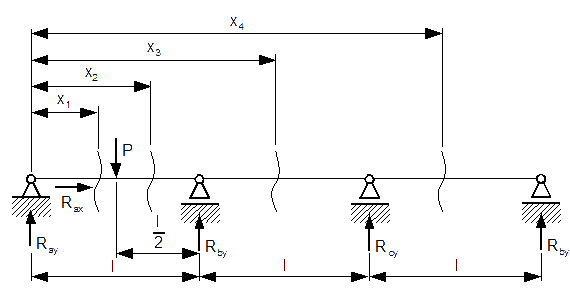
Dane:
![l=1[m]; P=1[kN]](rownania/w_433.gif)
Rozwiązanie:
Układy równań statycznej równowagi:
Należy obrać dwie reakcje statycznie niewyznaczalne, w tym przypadku wybrane zostały przeze mnie reakcje Ray oraz Rby. W pierwszej kolejności należy rozpisać równanie energetyczne dla reakcji Rby ponieważ leży ona pomiędzy podporami a oraz b. Jedyne dopuszczalne niewiadome w równaniu energetycznym dla reakcji Rby jest reakcja tejże podpory i reakcja Ray, wszystkie pozostałe niewiadome reakcje muszą zostać uzależnione od reakcji Rby, aby możliwe było otrzymanie poprawnego rozwiązania.
Układanie trzeciego równania dla reakcji Rby.
Przedział 3
Dlaczego od przedziału trzeciego? Ponieważ w równaniach M(x2) i M(x1) nie występuje Rby, więc pochodna po tej reakcji będzie równa zero, a co za tym idzie nie ma sensu ich rozpisywanie.
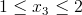
Przedział 4
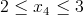
Sumowanie równań [27] oraz [30]:
Równanie [21] należy podstawić do równania [22]:
Układanie czwartego równania dla reakcji Ray.
Przedział 1
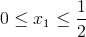
Przedział 2
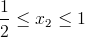
Przedział 3
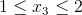
Przedział 4
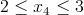 <
<
Sumę wyrażeń [35], [38], [41] oraz [44] należy przyrównać do zera i wyznaczyć wartość reakcji Ray:
Znając Ray można wyznaczyć Rby:
Znając Ray oraz Rby można wyznaczyć Rcy:
Znając Ray, Rby i Rdy można wyznaczyć Rdy:<
Obliczenia funkcji M(x) i T(x) po poszczególnych przedziałach.
Przedział 1
Przedział 2
Przedział 3
Przedział 4
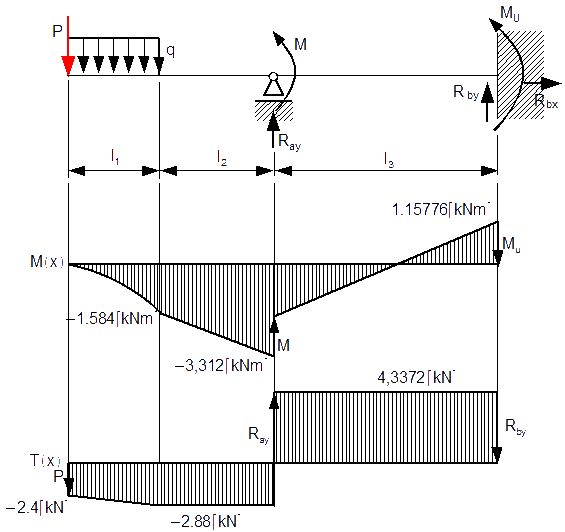
Wykresy.
Wyznaczyć reakcje belki jednokrotnie statycznie niewyznaczalnej z rysunku 5.
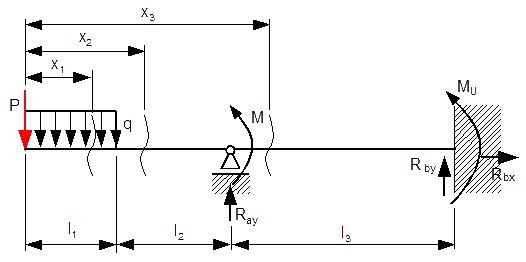
Dane:
![l_1=0.6[m]; l_1=0.6[m]; l_3=0.8[m]; q=0.8left[frac{kN}{m}\right]; P=2.4[kN]; M=-1[kNm]](rownania/w_498.gif)
Rozwiązanie:
Jest to najłatwiejszy przypadek zadania z belką statycznie niewyznaczalną z dwóch powodów: po pierwsze funkcje M(x1) oraz M(x2) nie zawierają reakcji Ray więc pochodna po tejże reakcji tychże funkcji będzie równa zero, ergo można te dwa przedziały pominąć w obliczeniach; po drugie reakcje utwierdzenia znajdują się na końcu belki w związku z tym nie trzeba będzie podstawiać (tak jak trzeba było to robić w poprzednich zadaniach) ponieważ jedyną niewiadomą w równaniu energetycznym będzie reakcja obrana za statycznie niewyznaczalną (czyli Ray).
Reakcje utwierdzenia Rby oraz Mu "wyjdą" przy okazji sporządzania wykresów momentów gnących i sił tnących belki, więc można darować sobie rozpisywanie równań równowagi i zabrać się za napisanie równania energetycznego.
Przedział 3
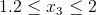
Wystarczy jedynie przyrównać otrzymaną wartość [60] do zera i wyznaczyć reakcję Ray i będzie można zabrać się za sporządzanie funkcji momentów gnących i sił tnących.
Równania momentów gnących i sił tnących.
Przedział 1
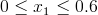
Położenie maksimum lub minimum lokalnego:
Określanie, czy w wyliczonym punkcie znajduje się maksimum czy minimum lokalne:
W wyliczonym punkcie znajduje się maksimum globalne funkcji M(x1).
Przedział 2
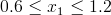
Przedział 3
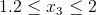
Sporządzanie wykresów.

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_431.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_432.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_434.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_435.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_437.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_438.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_439.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_441.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_442.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_443.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_445.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_446.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_447.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_448.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_449.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_450.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_451.gif)
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_452.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_453.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_454.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_455.gif)
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_456.gif)
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_457.gif)
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_458.gif)
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_460.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_461.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_462.gif)
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_464.gif)
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_465.gif)
![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_466.gif)
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_467.gif)
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_468.gif)
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_470.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_471.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_472.gif)
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_474.gif)
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_475.gif)
![Równanie [38]](https://obliczeniowo.com.pl/rownania/w_476.gif)
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_478.gif)
![Równanie [40]](https://obliczeniowo.com.pl/rownania/w_479.gif)
![R_{ay}cdot int_1^2left(2frac{1}{4}-1frac{1}{4}cdot x_3\right)cdot left(2frac{1}{4}-1frac{1}{4}cdot x_3\right)dx_3+Pcdot int_1^2left(frac{5}{8}cdot x_3-1frac{1}{8}\right)cdot left(2frac{1}{4}-1frac{1}{4}cdot x_3\right)dx_3=R_{ay}cdotint_1^2left(5frac{1}{16}-5frac{5}{8}cdot x_3+1frac{9}{16}cdot x_3^2\right)dx_3+Pint_1^2left(2frac{13}{16}cdot x_3-frac{25}{32}cdot x_3^2-2frac{17}{32}\right)dx_3=R_{ay}cdotleft[5frac{1}{16}cdot x_3-5frac{5}{8}cdot frac{1}{2}cdot x_3^2+1frac{9}{16}cdot frac{1}{3}cdot x_3^3\right]_1^2+Pcdot left[2frac{13}{16}cdot frac{1}{2}cdot x_3^2-frac{25}{32}cdot frac{1}{3}cdot x_3^3-2frac{17}{32}cdot x_3\right]_1^2=R_{ay}cdotleft(5frac{1}{16}cdot 2-2frac{13}{16}cdot 4+frac{25}{48}cdot 8-5frac{1}{16}+2frac{13}{16}-frac{25}{48}\right)+Pcdotleft(1frac{13}{32}cdot 4-frac{25}{96}cdot 8-2frac{17}{32}cdot 2-1frac{13}{32}+frac{25}{96}+2frac{17}{32}\right)=](https://obliczeniowo.com.pl/rownania/w_480.gif)
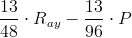
![Równanie [42]](https://obliczeniowo.com.pl/rownania/w_483.gif)
![Równanie [43]](https://obliczeniowo.com.pl/rownania/w_484.gif)
![Równanie [44]](https://obliczeniowo.com.pl/rownania/w_485.gif)
![Równanie [45]](https://obliczeniowo.com.pl/rownania/w_486.gif)
![Równanie [46]](https://obliczeniowo.com.pl/rownania/w_487.gif)
![Równanie [47]](https://obliczeniowo.com.pl/rownania/w_488.gif)
![Równanie [48]](https://obliczeniowo.com.pl/rownania/w_489.gif)
![Równanie [49]](https://obliczeniowo.com.pl/rownania/w_490.gif)
![Równanie [50]](https://obliczeniowo.com.pl/rownania/w_491.gif)
![Równanie [51]](https://obliczeniowo.com.pl/rownania/w_492.gif)
![Równanie [52]](https://obliczeniowo.com.pl/rownania/w_493.gif)
![Równanie [53]](https://obliczeniowo.com.pl/rownania/w_494.gif)
![Równanie [54]](https://obliczeniowo.com.pl/rownania/w_495.gif)
![Równanie [55]](https://obliczeniowo.com.pl/rownania/w_496.gif)
![Równanie [56]](https://obliczeniowo.com.pl/rownania/w_497.gif)
![Równanie [57]](https://obliczeniowo.com.pl/rownania/w_500.gif)
![Równanie [58]](https://obliczeniowo.com.pl/rownania/w_501.gif)
![-2.4cdot int_{1.2}^2x_3cdot (x_3-1.2)dx_3-0.8cdot 0.6cdot int_{1.2}^2(x_3-0.3)cdot (x_3-1.2)dx_3+int_{1.2}^2(x_3-1.2)^2dx_3+R_{ay}cdot int_{1.2}^2(x_3-1.2)^2dx_3=-2.4cdot left[frac{1}{3}cdot x_3^3-1.2cdot frac{1}{2}cdot x_3^2\right]_{1.2}^{2}-0.48cdot int_{1.2}^2(x_3^2-1.2cdot x_3-0.3cdot x_3+0.36)dx_3+left[frac{1}{2}cdot x_3^2-1.2cdot x_3\right]_{1.2}^2+R_{ay}cdot left[frac{1}{3}cdot x_3^3-2.4cdot x_3^2cdot frac{1}{2}+1.44cdot x_3\right]_{1.2}^2=-2.4cdot left(frac{1}{3}cdot 8-0.6cdot 4-frac{1}{3}cdot 1.728+0.6cdot 1.44\right)-0.48cdot left[frac{1}{3}cdot x_3^3-1.5cdot frac{1}{2}cdot x_3^2+0.36cdot x_3\right]_{1.2}^2+frac{1}{2}cdot 4-1.2cdot 2-frac{1}{2}cdot 1.44+1.2cdot 1.2+R_{ay}cdotleft(frac{1}{3}cdot 8-1.2cdot 4+1.44cdot 2-frac{1}{3}cdot 1.728-1.44cdot 1.2+1.2cdot 1.44\right)=](https://obliczeniowo.com.pl/rownania/w_502.gif)
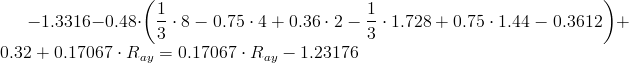
![Równanie [60]](https://obliczeniowo.com.pl/rownania/w_504.gif)
![Równanie [61]](https://obliczeniowo.com.pl/rownania/w_506.gif)
![Równanie [62]](https://obliczeniowo.com.pl/rownania/w_507.gif)
![Równanie [63]](https://obliczeniowo.com.pl/rownania/w_508.gif)
![Równanie [64]](https://obliczeniowo.com.pl/rownania/w_509.gif)
![Równanie [65]](https://obliczeniowo.com.pl/rownania/w_511.gif)
![Równanie [66]](https://obliczeniowo.com.pl/rownania/w_512.gif)
![Równanie [67]](https://obliczeniowo.com.pl/rownania/w_513.gif)
![Równanie [68]](https://obliczeniowo.com.pl/rownania/w_514.gif)