Rezystancja zastępcza w układach połączonych równolegle

Stronę tą wyświetlono już: 779 razy

W połączeniach równoległych elementów układu o znanej rezystancji odwrotność rezystancji zastępczej Rz jest równa sumie odwrotności rezystancji składowych, co można a nawet trzeba zapisać w następujący sposób:

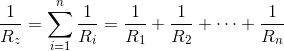1 / Rz = 1 / R1 + 1 / R2 + ... + 1 / Rn [1]

Zapis wyrażenia w formacie TeX-a:

\frac{1}{R_z}=\sum_{i=1}^{n}\frac{1}{R_i}=\frac{1}{R_1}+\frac{1}{R_2}+\dots+\frac{1}{R_n}

Powyższy wzór jest mało przydatny, albowiem bardziej interesuje mnie wzór na rezystancję zastępczą Rz niż na jej odwrotność:

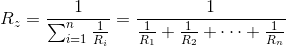R_z=1/(1 / R1 + 1 / R2 + ... + 1 / Rn) [2]

Zapis wyrażenia w formacie TeX-a:

R_z=\frac{1}{\sum_{i=1}^{n}\frac{1}{R_i}}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\dots+\frac{1}{R_n}}

Na poniższym rysunku można zobaczyć układ elementów połączonych w sposób równoległy.

Układ elementów połączonych równolegle
Rys. 1
Przykład układu elementów elektronicznych połączonych równolegle

Dla przykładu policzyć rezystancję zastępczą Rz układu trzech rezystorów R1 = 10 [Ω], R2 = 25 [Ω] i R3 = 50 [Ω].

Przykład układu trzech rezystorów połączonych równolegle, których rezystancję zastępczą należy obliczyć
Rys. 2
Przykład układu trzech rezystorów połączonych równolegle, których rezystancję zastępczą należy obliczyć

Rozwiązanie:

Rezystancja zastępcza rezystorów R1, R2 i R3 będzie równa:

R_z = 1 / (1 / 10 + 1 / 25 + 1 / 50) = 6 1/4 [Om-a] [3]

Zapis wyrażenia w formacie TeX-a:

R_z=\frac{1}{\sum_{i=1}^{n}\frac{1}{R_i}}=\frac{1}{\frac{1}{10}+\frac{1}{25}+\frac{1}{50}}=\frac{1}{\frac{5}{50}+\frac{2}{50}+\frac{1}{50}}=\frac{50}{8}=6\frac{1}{4}\,[\Omega]

Komentarze