Wyznaczanie środków ciężkości
Stronę tą wyświetlono już: 112782 razy
Środek ciężkości - punkt przyłożenia wypadkowej siły ciężkości lub punkt równowagi sił występujących w przekroju bryły poddawanej skręcaniu lub zginaniu.
Wyznaczenie środka ciężkości jest niekiedy możliwe z wykorzystaniem metody symetrii, która mówi że jeśli dane ciało ma oś symetrii, płaszczyznę symetrii lub punkt symetrii, to środek ciężkości leży na osi, płaszczyźnie oraz w punkcie symetrii.
Jeżeli dane ciało można podzielić na części, dla których w łatwy sposób można znaleźć (np. według zasady symetrii) współrzędne środka ciężkości to środek ciężkości takiego ciała można obliczyć korzystając z następującego wzoru:
gdzie:
- Vi - długość (dla odcinków); pole powierzchni (dla figur); objętość (dla brył) i-tego elementu składowego ciała, którego środek ciężkości jest liczony.
- Pi - położenie środka ciężkości elementu i-tego.
Jeżeli w danym ciele znajduje się pustka, możliwe jest wyznaczenie środka ciężkości tego ciała poprzez przyjęcie ujemnej wartości pola powierzchni lub objętości (w zależności od rodzaju obiektu) tejże pustki we wzorze [1].
Środek ciężkości trójkąta dowolnego
Przy okazji rozwiązywania zadania 2 z działu Układy przestrzenne statycznie wyznaczalne liczony był środek ciężkości płyty trójkątnej z użyciem wzoru na środek ciężkości trójkąta [2].
Środek ciężkości trójkąta dowolnego leży w odległości jednej trzeciej wysokości tego trójkąta licząc od boku, na który ta wysokość została spuszczona (rys 5). Powyższe stwierdzenie wynika właściwie z wzoru [2], aby tego dowieść należy przyjąć układ współrzędnych, dla którego oś X pokrywa się z danym bokiem trójkąta (jak na rysunku 5). W takim przypadku wzór [2] redukuje się dla współrzędnych Y-kowych do obliczenia jednej trzeciej wysokości tego trójkąta.
Ostatecznie więc uzyskuje się wzór na odległość środka ciężkości trójkąta dowolnego od dowolnego boku:
Wzory obliczeniowe
Istnieją wzory ogólne wyznaczające środek ciężkości brył, oraz figur płaskich. Wzory te mają następującą postać:
gdzie:
- ρ - gęstość, lub funkcja gęstości ciała (zazwyczaj przyjmuje się wartość 1);
- x, y, z - środek ciężkości elementarnej objętości V.
Licznik wzorów [4], [5] i [6] to statyczny moment ciała względem płaszczyzny układu współrzędnych XYZ. Mianownik to masa danego ciała (w zasadzie jest to objętość, ale przemnożona przez ρ daje oczywiście masę).
Zadanie 1
Wyznaczyć środek ciężkości trójkąta prostokątnego o wymiarach h na b.
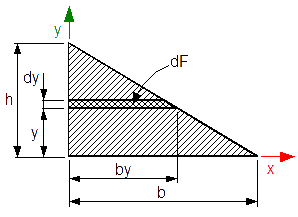
Rozwiązanie:
gdzie:
- My - statyczny moment figury względem osi y układu współrzędnych
Dla osi x liczenie tego samego nie ma sensu, ponieważ xc (przez analogię do obliczeń yc) jest równe:
Zadanie 2
Wyznaczyć środek ciężkości wycinka okręgu o promieniu R kącie β i kącie położenia α.
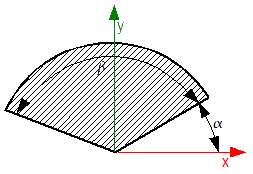
Rozwiązanie:
Tym razem całkowanie biegunowe, coby się nie przemęczać za bardzo z obliczeniami:
Zadanie 3
Korzystając z wyprowadzonych wzorów [16], [17] wyznaczyć środek półokręgu z rysunku 8.

Rozwiązanie:
Zadanie 4
Wyprowadzić wzór na środek ciężkości okręgu ściętego cięciwą jak na rysunku 9.
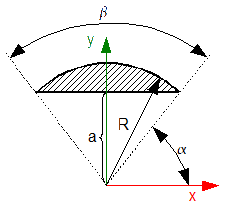
Rozwiązanie:
Górna granica całkowania to R, natomiast dolna:
a można wyznaczyć z następującej zależności:
tak więc dolna granica całkowania wynosi:
należy wyznaczyć wartość kąta α w zależności od kąta β:
granice całkowania dla kąta Φ:
Teraz można już przejść do głównej części zadania:
Ponieważ xc leży na osi y, nie ma sensu w tym przypadku liczyć dla niego środek ciężkości (zasada osi symetrii).
Zadanie 5
Obliczyć środek ciężkości przekroju belki z rysunku 10.

Rozwiązanie:
Rozwiązaniem będzie oczywiście całka po funkcji określającej krzywiznę przekroju belki:
Zadanie 6
Obliczyć środek ciężkości zbioru linii z rysunku 11.
Rozwiązanie:
środek ciężkości zbioru linii można wyznaczyć korzystając z wzoru [1], tak więc:
Zadanie 7
Obliczyć środek ciężkości figury płaskiej z rysunku 12 (należy skorzystać z wzoru [19] w celu określenia środka półokręgu).
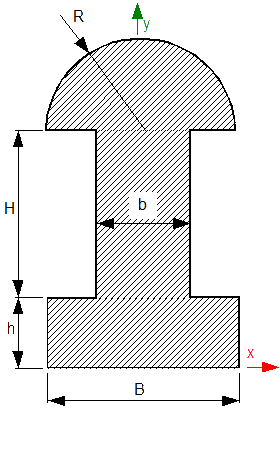
Dane:
![r=10[cm]; H=20[cm]; B=16[cm]; h=5[cm];b=6[cm]](rownania/w_246.gif)
Rozwiązanie:
Figura płaska z rysunku 12 ma oś symetrii, dlatego też przyjąć można położenie układu współrzędnych, tak aby oś y przechodziła przez środek symetrii. W ten sposób zadanie sprowadza się do znalezienia położenia środka ciężkości tylko na osi Y.
Zadanie 8
Obliczyć środek ciężkości figury płaskiej z rysunku 13.

Dane:
![b[cm]; h[cm]; r[cm]](rownania/w_248.gif)
Rozwiązanie:
Zadanie 9
Obliczyć środek ciężkości figury płaskiej z rysunku 14.
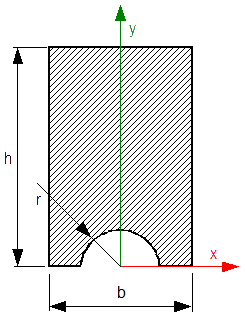
Dane:
![r=2[cm]; h=12[cm];b=8[cm]](rownania/w_250.gif)
Rozwiązanie:
Zadanie 10
Obliczyć środek ciężkości figury płaskiej z rysunku 15.

Rozwiązanie:
Zadanie 11
Obliczyć środek ciężkości figury płaskiej z rysunku 16.

Rozwiązanie:
Zadanie 12
Obliczyć środek ciężkości figury płaskiej z rysunku 17.
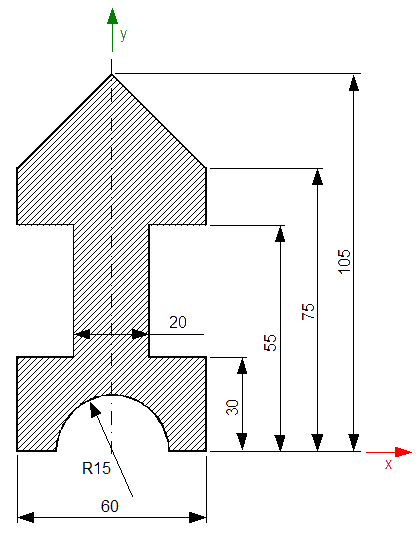
Rozwiązanie:
Zadanie 13
Wyznaczyć środek ciężkości stożka.
Rozwiązanie:
Należy znaleźć geometryczną zależność promienia r od promienia R, wysokości stożka H i położenia przekroju stożka z.
środek ciężkości stożka leży w odległości trzech czwartych jego wysokości licząc od wierzchołka.
Zadanie 14
Wyznaczyć środek ciężkości stożka ściętego.
Rozwiązanie:
Należy znaleźć geometryczną zależność promienia r od promieni RD, RG, wysokości stożka H i położenia przekroju stożka z.
Obliczenie masy obiektu o kształcie stożka ściętego:
Obliczenie statycznego momentu bezwładności obiektu w kształcie stożka ściętego:
Teraz ta łatwiejsza część zadania:
Zadanie 15
Wyznaczyć środek ciężkości wycinka kuli.
Rozwiązanie:
Wiedząc, że środek ciężkości bryły z osią symetrii leży w środku ciężkości przekroju tej bryły, przechodzącego przez oś jej symetrii wyznaczenie środka ciężkości wycinka kuli można obliczyć również ze wzorów [15], [17].
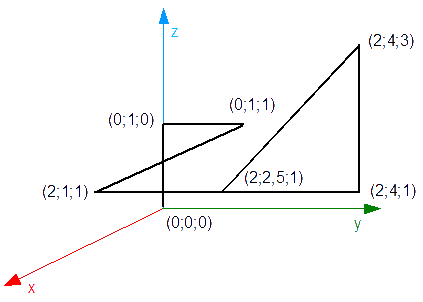
Zadanie 16
Obliczyć środek ciężkości wspornika z rysunku 21.
Rozwiązanie:
Dziabnąć trzeba wspornik na dwa prostopadłościany o masie dodatniej i cztery walce o masie ujemnej.

![Równanie [1]](https://obliczeniowo.com.pl/rownania/r_003.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/r_004.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/r_005.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/r_006.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/r_007.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/r_008.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_220.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_221.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_222.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_223.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_224.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_225.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_226.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_227.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_228.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_229.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_230.gif)
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_231.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_232.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_233.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_234.gif)
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_235.gif)
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_236.gif)
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_237.gif)
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_238.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_239.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_240.gif)
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_241.gif)
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_242.gif)
![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_243.gif)
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_244.gif)
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_245.gif)
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_247.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_249.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_251.gif)
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_252.gif)
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_253.gif)
![Równanie [38]](https://obliczeniowo.com.pl/rownania/w_254.gif)
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_255.gif)
![Równanie [40]](https://obliczeniowo.com.pl/rownania/w_256.gif)
![Równanie [41]](https://obliczeniowo.com.pl/rownania/w_257.gif)

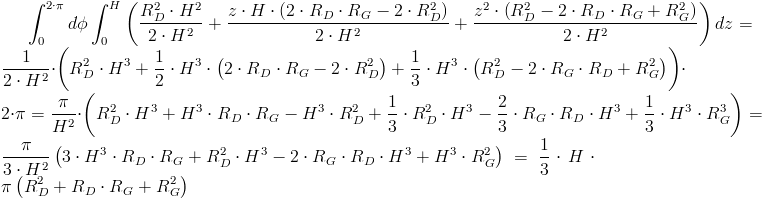
![M_z=/int_0^{2/cdot /pi}d/phi/int_0^Hz/, dz/int_0^{R_D-/frac{z/cdot /left( R__P-R_G/right)}{H}}r/, dr=/int_0^{2/cdot /pi}d/phi/int_0^H /frac{1}{2}/cdot/left(R_D^2-2/cdot /frac{z/cdot/left(R_D-R_G/right)/cdot R_D}{H}+/frac{z^2/cdot /left(R_D-R_G/right)^2}{H^2}/right)z/, dz=/frac{1}{2/cdot H^2}/cdot /int_{0}^{2/cdot /pi}d/phi/int_0^H/left(R_D^2/cdot H^2+z/cdot H/cdot /left(2/cdot R_D/cdot R_G-2/cdot R_D^2/right)+z^2/cdot /left(R_D^2-2/cdot R_G/cdot R_D+ R_G^2/right)/right)/cdot z/, dz=/frac{1}{2/cdot H^2}/cdot /int_0^{2/cdot /pi}d/phi/left[ /frac{1}{2}/cdot R_D^2/cdot H^2/cdot z^2+/frac{1}{3}/cdot z^3/cdot H/cdot /left(2/cdot R_D/cdot R_G-2/cdot R_D^2/right)+/frac{1}{4}/cdot z^4/cdot/left( R_D^2-2/cdot R_G/cdot R_D+R_G^2/right)/right]_{0}^{H}=/frac{/pi}{12/cdot H^2}/cdot/left(6/cdot R_D^2/cdot H^4+8/cdot H^4/cdot R_D/cdot R_G-8/cdot H^4/cdot R_D^2+3/cdot H^4/cdot R_D^2-6/cdot H^4/cdot R_G/cdot R_D+3/cdot H^4/cdot](https://obliczeniowo.com.pl/rownania/w_260.gif)
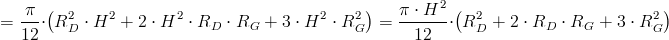
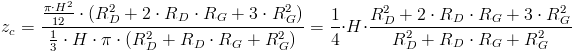

![M_z=/int_{/alpha}^{/frac{/pi}{2}}cos/theta/cdot sin/theta/, d/theta/int_0^{2/cdot /pi}d/phi/int_0^Rr^3/, dr=/frac{1}{2}/cdot /pi/cdot R^4 /cdot /int_{/alpha}^{/frac{/pi}{2}}cos/theta /cdot /sin/theta/, d/theta/begin{vmatrix}
cos/theta=t//
-sin/theta/, d/theta=dt//
sin/theta/, d/theta=-dt
/end{vmatrix}=/frac{2}{3}/cdot /pi /cdot R^4/cdot /int_{/alpha}^{2/cdot /pi}t/, dt=/frac{1}{2}/cdot /pi /cdot R^4/cdot /frac{1}{2} /cdot /left[-t^2/right]_{/alpha}^{2/cdot /pi}=/frac{1}{2}/cdot /pi /cdot R^4/cdot /frac{1}{2} /cdot /left(-cos^2 /frac{/pi}{2}+cos^2 /alpha /right) = /frac{1}{4}/cdot /pi /cdot R^4/cdot cos^2/alpha](https://obliczeniowo.com.pl/rownania/w_264.gif)

![x_c=/frac{7,5/cdot 15/cdot 40/cdot 55+40/cdot 50/cdot 40/cdot 15-55/cdot /pi /cdot 5^2/cdot 15-25/cdot /pi /cdot 5^2/cdot 15-7,5/cdot /pi /cdot 5^2/cdot 15-7,5/cdot /pi /cdot 5^2/cdot 15}{15/cdot 40/cdot 55+50/cdot 40/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15}/approx /frac{1335580,762}{58287,61102}/approx 22,91[mm]](https://obliczeniowo.com.pl/rownania/w_266.gif)
![y_c=/frac{20/cdot 15/cdot 40/cdot 55+20/cdot 50/cdot 40/cdot 15-10/cdot /pi /cdot 5^2/cdot 15-30/cdot /pi /cdot 5^2/cdot 15-10/cdot /pi /cdot 5^2/cdot 15-30/cdot /pi /cdot 5^2/cdot 15}{15/cdot 40/cdot 55+50/cdot 40/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15}/approx /frac{1165752,22}{58287,61102}/approx 20[mm]](https://obliczeniowo.com.pl/rownania/w_267.gif)
![z_c=/frac{27,5/cdot 15/cdot 40/cdot 55+7,5/cdot 50/cdot 40/cdot 15-7,5/cdot /pi /cdot 5^2/cdot 15-7,5/cdot /pi /cdot 5^2/cdot 15-25/cdot /pi /cdot 5^2/cdot 15-45/cdot /pi /cdot 5^2/cdot 15}{15/cdot 40/cdot 55+50/cdot 40/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15-/pi /cdot 5^2/cdot 15}/approx /frac{10332361,734}{58287,61102}/approx 17,71[mm]](https://obliczeniowo.com.pl/rownania/w_268.gif)