Statycznie wyznaczalne układy z tarciem
Stronę tą wyświetlono już: 20988 razy
Zadanie 1
Wyznaczyć siłę tarcia płyty o ciężarze Q spoczywającej na równi pochyłej jak na rysunku 1.
Dane:
![/alpha [^o]; Q[N]](rownania/w_194.gif)
Rozwiązanie:
Wystarczy nanieść wektory wypadkowe od ciężaru Q i wektor tarcia T, aby otrzymać rozwiązanie zadania.
Zadanie 2
Sprawdzić, czy dla podanego współczynnika tarcia układ z rysunku 2 pozostaje w spoczynku.
Dane:
![/mu =0,2; /alpha = 45^o; L=1,5[m]; H=1[m]; Q=1[kN]](rownania/w_195.gif)
Rozwiązanie:
Konieczne jest wyznaczenie tarcia T i nacisku N w celu określenia czy stosunek tarcia T do nacisku N jest mniejszy lub równy współczynnikowi tarcia podłoża.
Warunek pozostania w spoczynku:
Jak wynika z obliczeń, układ nie pozostanie w spoczynku.
Zadanie 3
Dla układu dwóch ciał połączonych nieważkim cięgnem jak na rysunku 3 obliczyć minimalną masę m1 aby układ pozostał w spoczynku.
Dane:
![/mu = 0,4[-]; m_2=200[kG]; g/approx 10/left[ /frac{m}{s^2}/right]](rownania/w_200.gif)
Rozwiązanie:
Obliczenie ciężaru Q2: oraz ciężaru Q1:Teraz można obliczyć nacisk N, który jest równy ciężarowi Q1, więc nie trzeba go liczyć lepiej się zająć wyznaczeniem tarcia T w zależności od masy m1.
Pozostało już tylko porównać stronami wyliczone siły:
Zadanie 4
Dla układu dwóch ciał połączonych nieważkim cięgnem jak na rysunku 4 obliczyć maksymalny ciężar Q1 umożliwiający pozostanie układu w równowadze.
Dane:

Rozwiązanie:
Zadanie 5
Dla układu dwóch ciał połączonych nieważkim cięgnem jak na rysunku 5 obliczyć maksymalny ciężar Q1 umożliwiający pozostanie układu w równowadze.
Dane:
![/mu _1=0,3[-]; /mu _2=0,4[-]; /alpha = 45^o;Q_2=6[kN]](rownania/w_207.gif)
Rozwiązanie:
Tym razem rozbiję ten układ na mniejsze podukłady, żeby wszystko było jasne:
Podukład 1
Podukład 2:
Podukład 3:
Zadanie 6
Dla układu z rysunku 6 obliczyć minimalną siłę Q2 niezbędną do utrzymania układu w stanie spoczynku.
Dane:
![/mu = 0,4; Q_1=50[kN]](rownania/w_211.gif)
Rozwiązanie:
Jak zwykle rozłożyć należy układ za części pierwsze.
Podukład I:
Podukład II:
Podukład III:
Zadanie 7
Dla układu z rysunku 8 obliczyć ciężar Q2 niezbędny do utrzymania układu w stanie spoczynku.
Dane:
![/mu =0,1[-]; Q_1=10[kN]](rownania/w_216.gif)
Rozwiązanie:
Podukład 1:
Podukład 2:
|
Pomiędzy siłami S1, S2 istnieje następująca zależność: |
Podukład 3:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_196.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_197.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_198.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_199.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_201.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_202.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_203.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_204.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_206.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_208.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_209.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_210.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_212.gif)
![T_1/cdot 2/cdot R- T_2/cdot 2/cdot R=0/Rightarrow T_2=75[kN]](https://obliczeniowo.com.pl/rownania/w_213.gif)

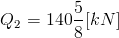
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_217.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_218.gif)
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_219.gif)