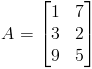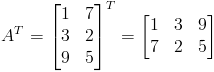Macierz transponowana
Stronę tą wyświetlono już: 1395 razy
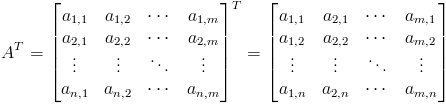
Macierz transponowana macierzy A jest przestawieniem argumentów macierzy A, takim że jej kolumny stają się wierszami a wiersze kolumnami w następujący sposób:
 | [1] |
Zapis wyrażenia w formacie TeX-a:
A^T=\begin{bmatrix}a_{1,1} & a_{1,2} & \cdots & a_{1,m}\\ a_{2,1} & a_{2,2} & cdots & a_{2,m}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n,1} & a_{n,2} & \cdots & a_{n,m}\end{bmatrix}^T=\begin{bmatrix} a_{1,1} & a_{2,1} & \cdots & a_{m,1}\\a_{1,2} & a_{2,2} & \cdots & a_{m,2}\\ \vdots & \vdots & \ddots & \vdots\\ a_{1,n} & a_{2,n} & \cdots & a_{m,n}\end{bmatrix}
Przykład
Wyznaczyć macierz transponowaną macierzy A.
Dane:
Rozwiązanie:
Warto też nadmienić, że wyznacznik macierzy kwadratowej A jest równy wyznacznikowi macierzy transponowanej AT.