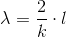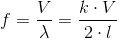Stronę tą wyświetlono już: 3630 razy

W muzyce wyróżnia się całą gamę instrumentów strunowych, które właśnie wykorzystują strunę dwustronnie podpartą do wytwarzania dźwięków o określonej częstotliwości. Co ciekawe ponieważ struna tego typu jest podparta, więc jej drgania muszą (i są) ściśle powiązane z długością odcinka podpartego struny. Oto bowiem punkty podparcia wymuszają powstawanie drgań akustycznych w takiej strunie o długość fali λ równej:

[1]

Zapis wyrażenia w formacie TeX-a:

\lambda=\frac{2}{k}\cdot l

gdzie:

• λ - długość fali akustycznej;
• l - długość struny;
• k - liczba naturalna różna od zera (1, 2, 3).

Obliczenie częstotliwości drgań takiej struny jest prostsza aniżeli odebranie dzieciakowi lizaka, albowiem wystarczy wykorzystać następujący wzór:

[2]

Zapis wyrażenia w formacie TeX-a:

f=\frac{V}{\lambda}=\frac{k \cdot V}{2\cdot l}

gdzie:

• λ - długość fali akustycznej;
• l - długość struny;
• k - liczba naturalna różna od zera (1, 2, 3);
• V - prędkość dźwięku rozprzestrzeniającego się w materiale, z jakiego zrobiona została struna.

No dobrze, ale jak to się dzieje do licha, że ta struna może wydawać tylko takie a nie inne dźwięki? Żeby odkryć tą tajemnicę należy zerknąć łaskawym okiem na poniższą ilustrację, na której widać, że struna musi drgać w taki sposób aby na jej końcach wartość wychyleń była równa zero.