Macierze obrotu

Stronę tą wyświetlono już: 4633 razy

Temat ten był już poniekąd omawiany w dziale Matematyka → Wektory → Obrót wektora o kąt, z tego też powodu samo wyprowadzenie oraz słuszność wzorów tutaj użytych do stworzenia macierzy obrotu nie będzie tutaj omawiana po raz kolejny. Tych więc, którzy są zainteresowani szczegółami związanymi z wyprowadzeniem odsyłam do wcześniej wspomnianej strony.

Macierz obrotu w przestrzeni 2W

Istnieje taka grupa szczególnych macierzy, zwanych macierzami obrotu Mo, która umożliwia poprzez mnożenie macierzowe z wektorem V tego samego wymiaru n uzyskanie nowego wektora V', który został obrócony względem początku układu współrzędnych o zadany kąt α.

Macierz obrotów Mo dla danego kąta α w przestrzeni 2W przyjmuje postać następującą:

Równanie [1] [1]

Obrócenie wektora, tak jak to wcześniej wspomniałem można wykonać poprzez zwykłe mnożenie macierzowe w następujący sposób:

Równanie [2] [2]

Na poniższym rysunku można zobaczyć przykładowy obrót figury płaskiej względem początku układu współrzędnych.

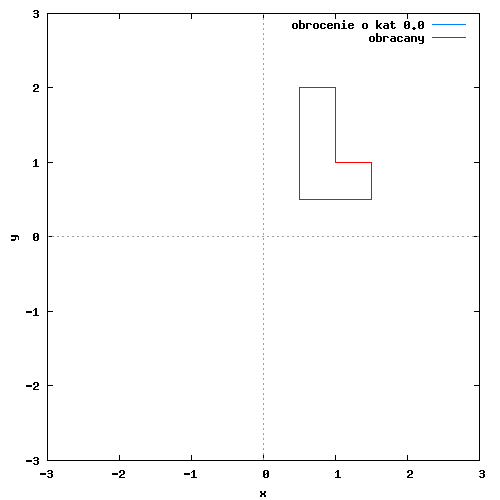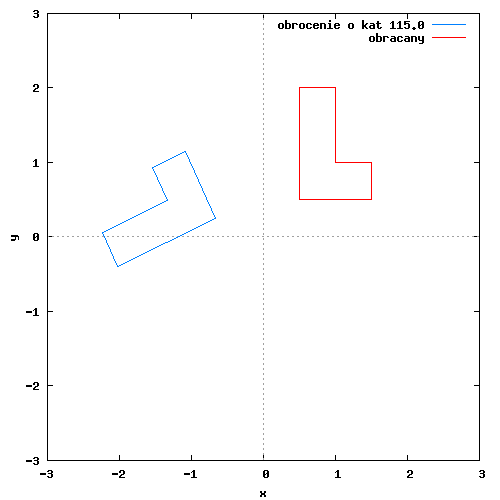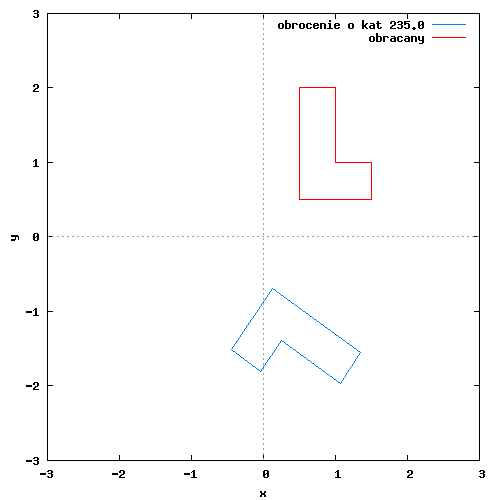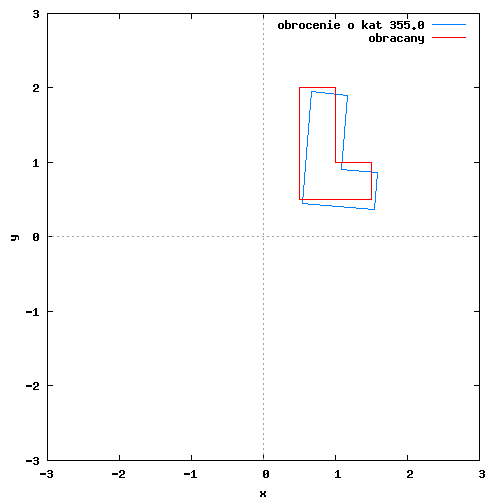
Animacja obrotu przykładowego obiektu o zadany kąt.
Rys. 1
Animacja obrotu przykładowego obiektu o zadany kąt.

Poszczególne klatki animacji wygenerowane zostały w programie wxMaxima za pomocą następującego kodu:

Listing 1
  1. x1:2;
  2. y1:1;
  3. xo: 2;
  4. yo: 0;
  5. da: 5 * %pi / 180;
  6. v: matrix([x1],[y1]);
  7. ik: matrix([xo], [yo]) * 1 / sqrt(xo^2+yo^2);
  8. jk: matrix([-ik[2][1]],[ik[1][1]]);
  9. obj:matrix([0.5,1.5,1.5,1,1,0.5,0.5],[0.5,0.5,1,1,2,2,0.5]);
  10. Mk: matrix([ik[1][1], jk[1][1]],[ik[2][1], jk[2][1]]);
  11. obj2: float(Mk . obj);
  12. l: float(sqrt(v2[1][1]^2+v2[2][1]^2)-sqrt(v[1][1]^2+v[2][1]^2));
  13. Mrot: float(matrix([cos(da), -sin(da)],[sin(da),cos(da)]));
  14. i:0;
  15. for i: 0 thru 71 do(
  16. Mk: matrix([ik[1][1], jk[1][1]],[ik[2][1], jk[2][1]]),
  17. obj2: float(Mk . obj),
  18. ik: Mrot . ik,
  19. jk: Mrot . jk,
  20. plot2d([[discrete, obj2[1], obj2[2]], [discrete, obj[1], obj[2]]],[x,-3,3],[y,-3,3],[gnuplot_term, "png size 500,500"], [gnuplot_out_file, printf(false,"C:\\obr2 ~f.png",i)],[legend,printf(false,"obrocenie o kat ~f",da*i/%pi * 180),"obracany"])
  21. )$

Animacja poskładana w programie Gimp

Tę samą operację można wykonać względem dowolnego punktu, wystarczy tylko nieco zmodyfikować wzór [2]:

Równanie [3] [3]

Istnieją szczególne rodzaje macierzy obrotów Mo, do których należą obroty o krotność kąta 90°. Tak więc dla obrotu o 90° macierz obrotów Mo ma następującą postać:

Równanie [4] [4]

Dla 270° a tym samym dla -90° macierz obrotu ma postać następującą:

Równanie [5] [5]

I nareszcie, macierz obrotu Mo o 180°:

Równanie [6] [6]

Macierze obrotu w przestrzeni 3W

Obroty trójwymiarowe, które również zostały omówione na stronie Matematyka → Wektory → Obrót wektora o kąt, można wykonywać w zasadzie na podstawie tego samego wzoru [1] z lekką modyfikacją i tylko względem danej osi układu współrzędnych.

Macierz obrotu dla osi z w układzie 3W:

Równanie [7] [7]

Na poniższej animacji można zobaczyć przykładowy obrót obiektu względem osi z.

Animacja obrotu przykładowego obiektu względem osi z.
Rys. 2
Animacja obrotu przykładowego obiektu względem osi z.

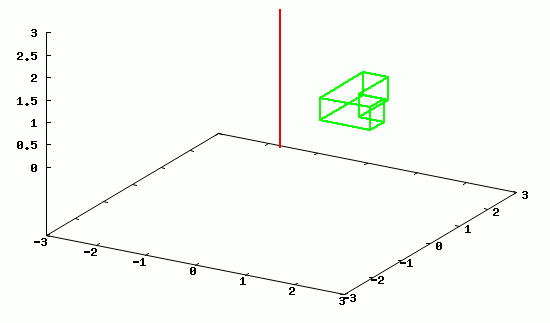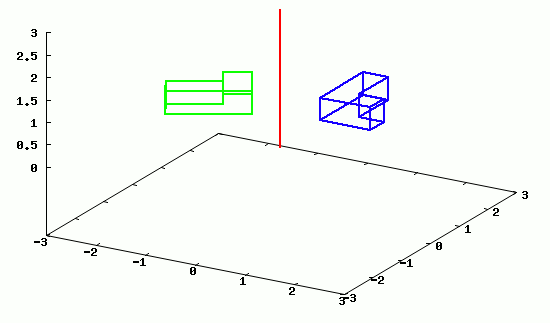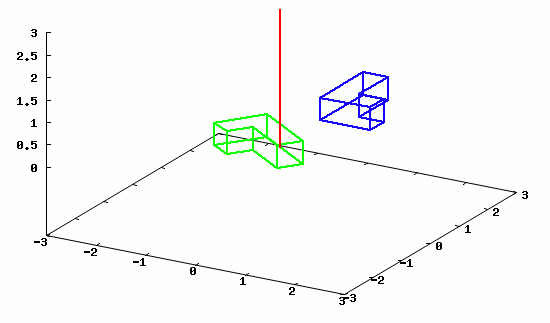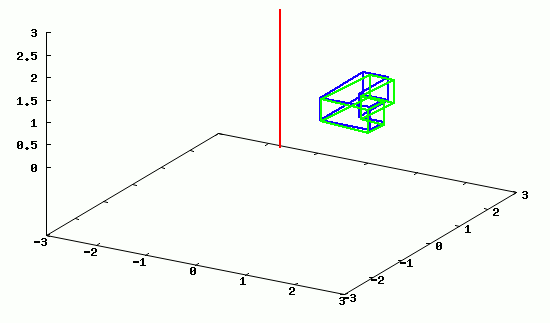
Poszczególne klatki animacji wygenerowane w programie wxMaxima

Animacja poskładana w programie Gimp

Macierz obrotu dla osi y w układzie 3W:

Równanie [8] [8]

Macierz obrotu dla osi x w układzie 3W:

Równanie [9] [9]

Składanie macierzy obrotu w układach 3W

Istnieje również możliwość składania obrotów względem np. osi x, y i osi z. Taka operacja będzie miała następującą przykładową postać dla przykładowego obrotu względem osi x i z:

Równanie [10] [10]

Cechy macierzy obrotu Mo

Każda macierz obrotu Mo jest macierzą ortogonalną i jako taka spełnia określone warunki:

1) Wartość wyznacznika macierzy obrotu Mo zawiera się w przedziale |M0|∈{-1; 1}

2) Transpozycja macierzy obrotu MoT jest równa macierzy Mo-1:

Równanie [11] [11]

3) Iloczyn macierzy obrotu Mo z jej transpozycją MoT daje w wyniku macierz jednostkową:

Równanie [12] [12]
Tematy powiązane

Komentarze