Wykresy momentów gnących i sił tnących w belkach statycznie wyznaczalnych
Stronę tą wyświetlono już: 51149 razy
Sporządzenie wykresów momentów gnących M(x), sił tnących T(x) oraz podłużnych N(x) umożliwia odnalezienie maksymalnego obciążenia momentem gnącym, siłą tnącą i podłużną danej belki (i nie tylko belki). W tym dziale omówione zostaną sposoby tworzenia tych wykresów dla belek statycznie wyznaczalnych.
Wykres momentów gnących M(x) określa wartość momentu gnącego występującego w przekroju znajdującego się w danej odległości x najczęściej od początku lewej strony belki.
Wykres sił tnących T(x) - określa wartość siły tnącej (prostopadłej do belki) działającej w danej odległości x najczęściej od początku lewej strony belki. Często funkcję T(x) uzyskuje się poprzez obliczenie pochodnej funkcji momentów gnących M(x) po dx czyli w następujący sposób:
Wykres sił poprzecznych N(x) - określa siłę działającą na belkę w danej odległości x najczęściej od początku lewej strony belki.
Sporządzić wykres momentów gnących i sił tnących belki z rysunku 1
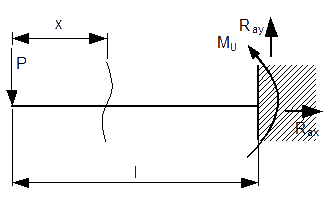
Dane:
![l[m]; P[N]](rownania/w_347.gif)
Rozwiązanie:
Nasza belka została podzielona na jeden przedział, w którym x zmienia się w zakresie od 0 do l, czyli przedział zaczyna się od początku lewej strony belki a kończy się na końcu tejże belki. Dla przedziału tego napisać należy funkcję M(x) w następujący sposób:
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_348.gif) | [2] |
Zapis wyrażenia w formacie TeX-a:
Jak widać, od razu obliczyłem wartości na krańcach przedziału, aby w łatwy sposób móc sporządzić wykres momentów gnących. Wartość na końcu przedziału jest równa momentowi utwierdzenia MU belki.
Funkcję T(x) można uzyskać, poprzez zastosowanie wzoru [1] w następujący sposób:
Dla wykresu funkcji T(x) nie ma co liczyć wartości na krańcach przedziału, ponieważ przyjmuje ona wartość stałą równą -P. Pozostało jedynie sporządzenie wykresów.
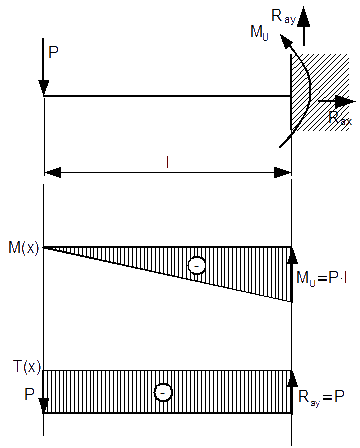
Sporządzić wykres momentów gnących i sił tnących belki z rysunku 2.
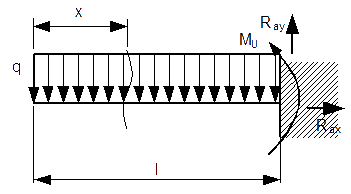
Dane:
![l[m]; qleft[frac{N}{m}right]](rownania/w_350.gif)
Rozwiązanie:
Po raz drugi mamy tu do czynienia z belką jedno przedziałową, jedyną różnicą jest oczywiście zastosowanie tutaj obciążenia równomiernego q. Zaczynamy wyznaczenia od funkcji M(x):
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_351.gif) | [4] |
Zapis wyrażenia w formacie TeX-a:
a następnie funkcji T(x)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_352.gif) | [5] |
Zapis wyrażenia w formacie TeX-a:
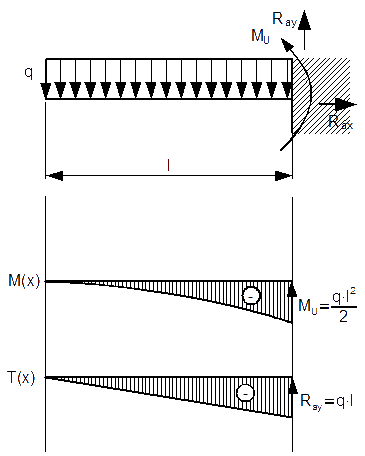
Funkcja M(x) jest funkcją kwadratową, więc należy dla niej określić maksimum, lub minimum tejże funkcji. Jako że maksimum lub minimum leży zawsze w miejscach zerowych danej funkcji, więc w naszym przypadku minimum lub maksimum leży w punkcie x=0, ponieważ dla x=0 pochodna funkcji M(x) jest równa zero. Określenie, czy w danym punkcie znajduje się minimum czy maksimum umożliwia obliczenie drugiej pochodnej funkcji M(x) po x-sie. Jeżeli uzyskana wartość w naszym punkcie będzie mniejsza od zera, to mamy do czynienia z maksimum lokalnym lub globalnym, w przeciwnym razie z minimum lokalnym lub globalnym.
Co prawda w przypadku tego zadania można się domyślić gdzie jest minimum czy też maksimum funkcji, jednakże przy bardziej złożonych funkcjach obciążenia ciągłego obliczanie pochodnych pierwszej i drugiej ma już duże znaczenie. Dobrze, druga pochodna po x-sie z M(x) to -q, czyli wartość ujemna, w x=0 funkcja ma maksimum lokalne.
Pozostało jedynie sporządzenie wykresów, co też i czynię na rysunku 4.
Sporządzić wykres momentów gnących i sił tnących belki z rysunku 5.
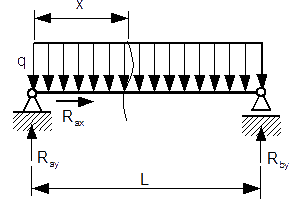
Dane:
![l[m]; qleft[frac{N}{m}right]](rownania/w_350.gif)
Rozwiązanie:
To już ostatnie zadanie z belką jedno-przedziałową. W tym przypadku najsamprzód trzeba wyznaczyć reakcję Ray naszej belki. Wyznaczenie reakcji Rax nie ma sensu, ponieważ wiemy że jest ona równa zero. Tak więc zabieramy się za wyznaczenie reakcji Ray:
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_353.gif) | [6] |
Zapis wyrażenia w formacie TeX-a:
Reakcja Ray jest już znana więc można napisać równanie momentów gnących M(x):
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_354.gif) | [7] |
Zapis wyrażenia w formacie TeX-a:
Funkcja M(x) na krańcach przedziału ma wartości równe zero, oznacza to, że gdzieś pomiędzy tymi przedziałami znajduje się albo maksimum, albo minimum globalne tej funkcji. Zanim wyznaczony zostanie maksimum, obliczymy pochodną funkcji M(x) do x-sie uzyskując oczywiście jak już nam wiadomo funkcję T(x) (która jest potrzebna również do wyznaczenia maksimum funkcji):
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_355.gif) | [8] |
Zapis wyrażenia w formacie TeX-a:
Należy znaleźć miejsce zerowe funkcji T(x):
W odległości równej połowie długości l naszej belki znajduje się maksimum lub minimum funkcji, a by się dowiedzieć czy maksimum czy minimum liczymy drugą pochodną z funkcji M(x) po x-sie i sprawdzamy jej wartość:
Na podstawie zależności [10] można stwierdzić ponad wszelką wątpliwość, że w połowie długości l< belki znajduje się maksimum globalne, którego wartość należy policzyć.
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_358.gif) | [11] |
Zapis wyrażenia w formacie TeX-a:
Pozostało już tylko sporządzenie wykresów momentów gnących:
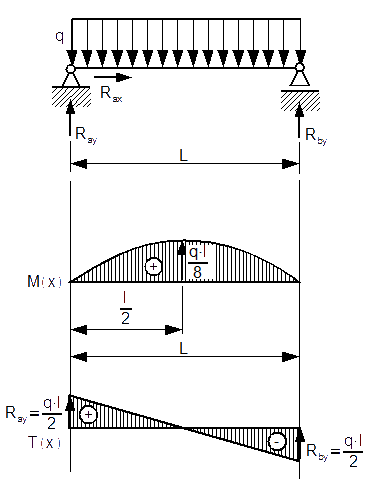
Sporządzić wykres momentów gnących i sił tnących belki z rysunku 6.
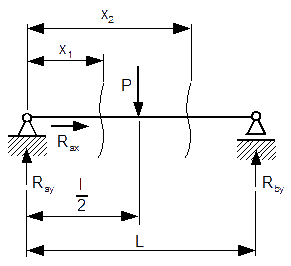
Dane:
![l[m]; qleft[frac{N}{m}right]](rownania/w_350.gif)
Rozwiązanie:
Tak jak zostało to przyobiecane w poprzednim zadaniu koniec z prostymi belkami jedno-przedziałowymi, czas na prostą belkę dwu-przedziałową. Pierwszy przedział
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_359.gif) | [12] |
Zapis wyrażenia w formacie TeX-a:
Reakcja Ray została już wyznaczona, więc zaczynamy zabawę z funkcjami dla pierwszego przedziału:
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_360.gif) | [13] |
Zapis wyrażenia w formacie TeX-a:
Funkcje M(x2) i T(x2) dla przedziału drugiego:
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_362.gif) | [15] |
Zapis wyrażenia w formacie TeX-a:
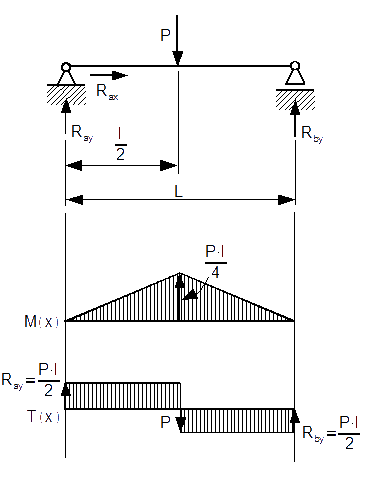
Sporządzić wykres momentów gnących i sił tnących belki z rysunku 9.
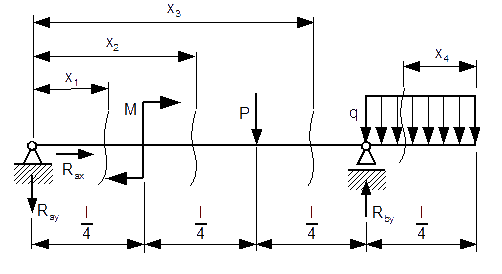
Dane:
![l=4[m]; q=10^4left[frac{N}{m}right]; P=10^4[N];M=10^4[Nm]](rownania/w_364.gif) <
<
Rozwiązanie:
Jak widać na załączonym rysunku zabawa się skończyła, czas na rozwiązanie porządnej belki statycznie wyznaczalnej i sporządzenie wykresów momentów gnących i sił tnących. W tym przypadku niestety konieczne jest obliczenie reakcji Ray:
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_365.gif) | [17] |
Zapis wyrażenia w formacie TeX-a:
Zaczynamy zabawę w tworzenie funkcji dla poszczególnych przedziałów:
Przedział 1
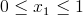
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_367.gif) | [18] |
Zapis wyrażenia w formacie TeX-a:
Przedział 2
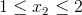
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_370.gif) | [20] |
Zapis wyrażenia w formacie TeX-a:
Przedział 3
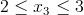
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_373.gif) | [22] |
Zapis wyrażenia w formacie TeX-a:
Przedział 4
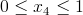
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_376.gif) | [24] |
Zapis wyrażenia w formacie TeX-a:
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_377.gif) | [25] |
Zapis wyrażenia w formacie TeX-a:
Ponieważ przedział czwarty liczymy od drugiej strony belki, wartości funkcji T(x4) należy na wykresie zaznaczyć z przeciwnym znakiem. Konieczne jest jeszcze określenie maksimum funkcji M(x4).
I jeszcze sprawdźmy, czy to jest minimum czy maksimum:
czyli maksimum globalne (bo to funkcja kwadratowa to inne nie może być maksimum).
Wykresy jak zwykle na koniec.
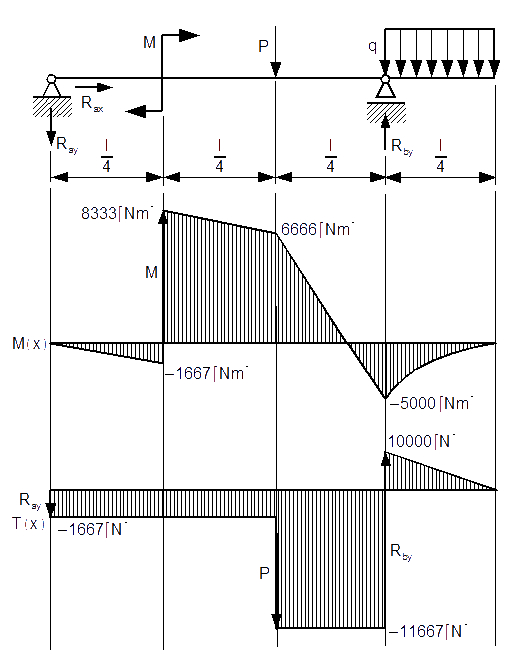
Dane:
![l=3[m]; q=5cdot 10^3left[frac{N}{m}right];P=10^4[N]](rownania/w_380.gif)
Rozwiązanie:
Niestety trzeba rozłożyć ten układ na dwa podukłady, i obliczyć co najmniej dwie reakcje podpór Rdy i Ray oraz jedną reakcję Rcy występującą w przegubie. No ale jak powiedział Predator do swego oprawcy zanim odciął sobie łapę "Życie jest do dupy".
Podukład 1
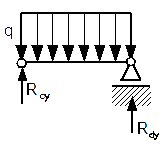 |
Podukład 2
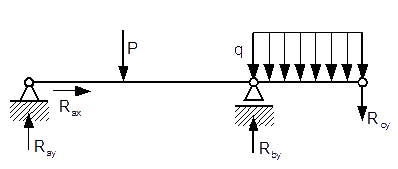 |
Zaczynamy rozpisywanie funkcji momentów gnących M(x) i sił tnących T(x) dla poszczególnych przedziałów.
Przedział 1

![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_385.gif) | [31] |
Zapis wyrażenia w formacie TeX-a:
Przedział 2
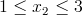
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_388.gif) | [33] |
Zapis wyrażenia w formacie TeX-a:
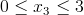
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_391.gif) | [35] |
Zapis wyrażenia w formacie TeX-a:
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_392.gif) | [36] |
Zapis wyrażenia w formacie TeX-a:
Trzeba jeszcze znaleźć maksimum lub minimum globalne funkcji M(x3).
Wiemy gdzie, nie wiemy co, no to się dowiemy na podstawie drugiej pochodnej:
i już wiadomo, że maksimum teraz należy obliczyć wartość tego maksimum:
No i jeszcze wykresy jak zwykle na koniec trzeba narysować, co też i czynię z najdzikszą rozkoszą.
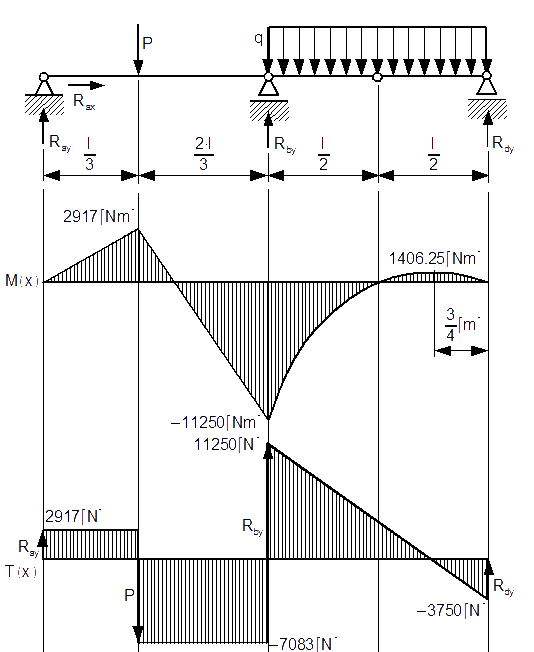

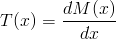
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_349.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_356.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_357.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_361.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_363.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_368.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_371.gif)
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_374.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_378.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_379.gif)
![sum M_{c}=0: R_{dy}cdot frac{l}{2}-qcdot frac{l^2}{8}=0Rightarrow R_{dy}=3750[N]](https://obliczeniowo.com.pl/rownania/w_381.gif)
![sum M_{d}=0: R_{cy}cdot frac{l}{2}-Qcdot frac{l^2}{8}=0Rightarrow R_{cy}=3750[N]](https://obliczeniowo.com.pl/rownania/w_382.gif)
![sum M_{by}=-R_{ay}cdot l+frac{2}{3}cdot lcdot P-qcdot frac{l}{2}cdot frac{l}{4}-qcdot frac{l}{8}=0Rightarrow R_{ay}=2917[N]](https://obliczeniowo.com.pl/rownania/w_383.gif)
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_386.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_389.gif)
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_393.gif)
![Równanie [38]](https://obliczeniowo.com.pl/rownania/w_394.gif)
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_395.gif)