Całki oznaczone
Stronę tą wyświetlono już: 10711 razy
Zanim zacznę tłumaczyć czym jest całka oznaczona rozważmy konstrukcję obliczania pola powierzchni zawartej pomiędzy osią x a dowolną funkcją f(x) w przedziale od a do b (jak na rysunku 1). Obszar można podzielić na n prostokątów, których szerokość Δ będzie równa:
zaś wysokość owego prostokąta będzie równa wartości funkcji f(x_i), gdzie xi jest równe:
gdzie:
- i∈{1,2,..,n-1}
Wzór na całkowitą przybliżoną wartość pola powierzchni zawartej pomiędzy funkcją f(x) a osią x w przedziale od a do b można zapisać jako sumę elementarnych prostokątów:
Im większy jest podział, a więc im większe jest n tym więcej prostokątów o mniejszej szerokości Δx im więcej prostokątów tym dokładniejszy wynik. Reasumując, gdy n→∞ to Δx→0 i różnica pomiędzy rzeczywistym polem powierzchni a wyliczonym równa się 0. Pytanie zagadka to jak zsumować nieskończenie wiele prostokątów o nieskończenie małej szerokości aby uzyskać dokładny wynik? Odpowiedzią na to pytanie jest operator całki oznaczonej.
Całka oznaczona stanowi różnicę dowolnych funkcji pierwotnych F(b)-F(a), gdzie a - dolna granica całkowania, b górna granica całkowania. Zapis matematyczny jest więc następujący:
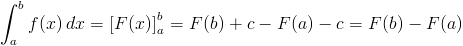 | [4] |
Zapis wyrażenia w formacie TeX-a:
Graficznie wynik działania [4] można obejrzeć na rysunku 2. Całkowanie umożliwia nie tylko pól powierzchni obliczanie ale również objętości, długości odcinków funkcji, środków ciężkości, momentów bezwładności.
 |
Całka oznaczona z funkcji, której wykres znajduje się poniżej osi x ma ujemną wartość pola powierzchni. W przypadku gdy wykres funkcji w przedziale <a, b> przebiega poniżej jak i powyżej osi x jej wartość jest równa różnicy pól powierzchni znajdujących się powyżej i poniżej osi x. |

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1577.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1579.gif)
