Kratownice statycznie wyznaczalne - rozwiązywanie metodą graficzną planu sił Cremony
Stronę tą wyświetlono już: 22610 razy
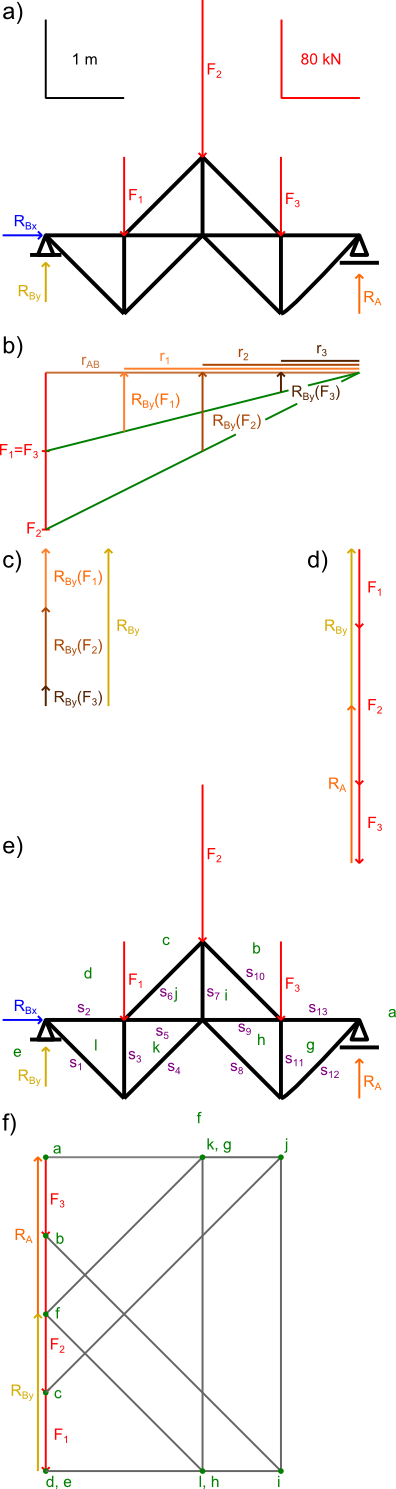
Nadeszła wiekopomna chwila, aby zacząć rozwiązywać kratownice statycznie wyznaczalne metodą graficzną planu Cremony. Najpierw rozwiążę tutaj bardzo prosty przykład, a nieco później rozwiążę przykład nieco trudniejszy.
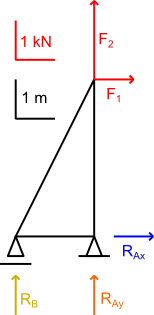
Najpierw konieczne jest naniesienie na powyższy rysunek oznaczeń promieni, na których działają siły czynne i reakcje względem punktu A, ponieważ odległości te będą potrzebne do graficznego wyznaczenia reakcji RB.
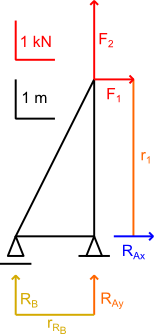
Teraz można się oddać spokojnej przyjemności wyznaczenia reakcji RB, ponieważ znane są już promienie rRB oraz r1 można zastosować tutaj konstrukcję graficznego mnożenia z dzieleniem, która opisana została na stronie Matematyka → Geometria → Twierdzenie Talesa na rysunku 12.
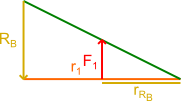
Korzystając ze skali z rysunku 1 można odczytać wartość reakcji RB, która wynosi -2 kN.
Teraz, z najdzikszą wręcz rozkoszą oddaję się graficznemu dodawaniu wszystkich sił czynnych i reakcji działających na kratownicę w osi y.

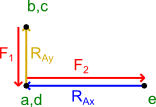
Z powyższej ilustracji wynika, że siła F1 jest całkowicie kompensowana przez reakcję RB a co za tym idzie reakcja RAy jest równa 0.
Czas "obliczyć" sumę sił i reakcji na osi x co też i z najdzikszą wręcz rozkoszą uczyniłem na poniższej ilustracji.
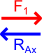
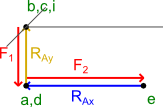
Z powyższej ilustracji wynika niezbicie, że reakcja RAx musi i równa się sile F1 z przeciwnym zwrotem.
Wprowadzam dodatkowe oznaczenia pól powierzchni, które oddzielają reakcje, siły czynne oraz siły wewnątrz prętów a także oznaczenia poszczególnych prętów kratownicy.
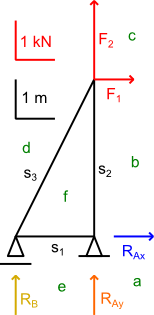
Na podstawie rysunku 6 należy narysować wielobok sił czynnych i reakcji podpór, gdzie dana siła lub reakcja ma początek i koniec w punktach oznaczonych nazwami pól, z którymi dana siła lub reakcja podpory sąsiaduje. Dla przykładu, reakcja RAx sąsiaduje z polem a i polem b, dlatego też narysowany jej wektor ma punkty krańcowe oznaczone jako a oraz b. Z punktu b wychodzi siła F1, która kończy się w punkcie c, ponieważ siła F1 sąsiaduje z polem b oraz polem c. Z punktu c wychodzi siła F2, która z kolei kończy się w punkcie d, a to dlatego, że siła F2 sąsiaduje z polem c oraz z polem d. Z punktu d wychodzi reakcja RB, która kończy się w punkcie e, ponieważ reakcja RB sąsiaduje z polem d oraz z polem e. Reakcja RAy, której wartość jest równa 0, zaczyna się w punkcie e i kończy w punkcie a, ponieważ sąsiaduje ona z polem e oraz z polem a.
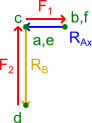
Bazując na rysunku 6 oraz rysunku 7 wyznaczę graficznie siły w prętach s1, s2 i s3. Siły w prętach s1, s2 i s3 wyznacza się poprzez wykreślenie linii równoległych do linii tych prętów, które należy poprowadzić z punktu, z którego polem dany pręt sąsiaduje. Dla przykładu pręt s1 sąsiaduje z polem e, więc z punktu e należy poprowadzić prostą równoległą do pręta s1. Teraz dla pręta s2 z punktu b należy również poprowadzić prostą równoległą do tegoż pręta. Punkt przecięcia się obu prostych wyznacza punkt f. Pozostało jeszcze poprowadzenie prostej z punktu d, która będzie odpowiadała prętowi s3. Jeżeli wszystko zostało dobrze rozrysowane, to prosta ta powinna przeciąć punkt f.
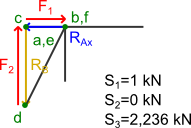
Jak odczytać siły w prętach? Prosto, należy zobaczyć, z którymi polami powierzchni dany pręt sąsiaduje, np. pręt s1 sąsiaduje z polem e oraz polem f, w związku z czym na powyższym wykresie mierzę odległość od punktu e do punktu f (oczywiście w obranej skali) i otrzymana wartość mówi nam o sile, jaka działa na ten pręt. To samo tyczy się prętów s2 oraz s3.
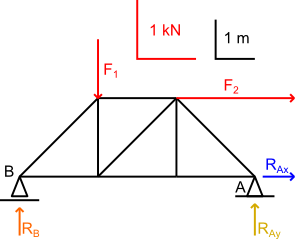
Rozwiążę jeszcze jedno, nieco trudniejsze zadanko z rysunku 9.
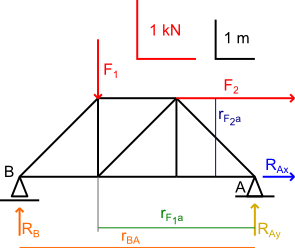
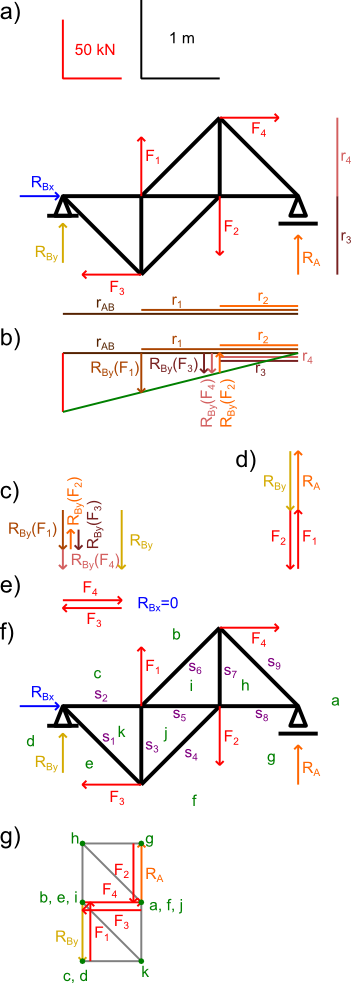
Nanoszę pomocnicze oznaczenia na rysunek 9.
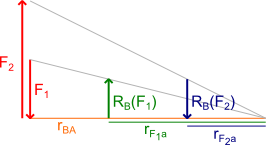
Graficzne wyznaczanie składowych reakcji RB(F1) oraz RB(F2).
Suma reakcji składowych RB(F1) oraz RB(F2) jest równa reakcji RB podpory przesuwnej B, a więc graficznie wygląda to tak jak na poniższym rysunku.
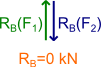
Suma sił czynnych i reakcji na osi y

Suma sił czynnych i reakcji na osi x
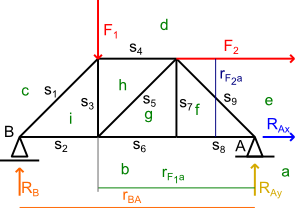
Wprowadzenie oznaczeń pól powierzchni i prętów na kratownicę z rysunku 9.
Kreślenie wieloboku sił czynnych i reakcji podpór.
Wyznaczenie punktu i za pomocą prętów s1 i s2.
Wyznaczanie punktu h za pomocą prętów s3 i s4.
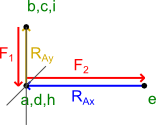
Wyznaczanie punktu g za pomocą prętów s5 i s6.
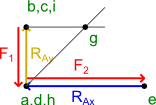
Wyznaczanie punktu f za pomocą prętów s7 i s8.
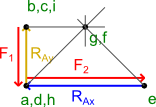
Odczyt wartości sił z uwzględnieniem skali odbywa się poprzez znalezienie pól powierzchni, z którymi dany pręt sąsiaduje i zmierzeniu odległości od tych punktów na rysunku 20. Dla przykładu pręt s9 sąsiaduje z polem e oraz z polem f a odległość pomiędzy tymi punktami na rysunku 20 z uwzględnieniem skali wynosi 1,4 kN. Podobnie odczytać można a nawet trzeba siły w pozostałych prętach.
Kolejne zadanie rozwiązane już bez zbędnego rozpisywania się co i jak.
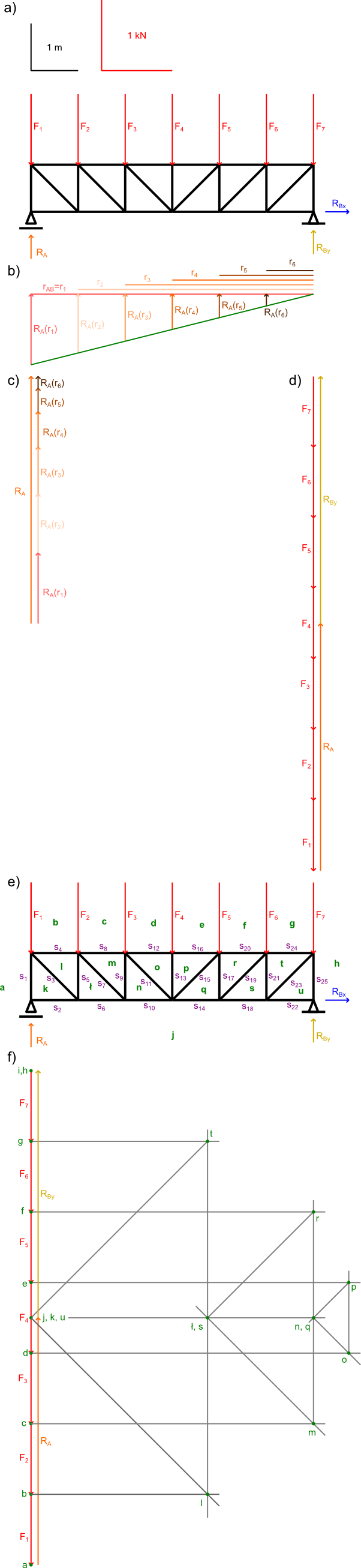
I jeszcze jedno zadanie.
I kolejne zadanie.