Cykloidy
Stronę tą wyświetlono już: 12741 razy
Definicja
Cykloidą nazywa się trajektorię ruchu punktu umieszczonego na obwodzie koła toczącego się bez poślizgu po płaskiej powierzchni.
Bardziej ogólna definicja: cykloida to taka krzywa, którą kreśli punkt umieszczony w obrębie a nawet poza obrębem takiego koła w stałej niezerowej odległości od jego środka, tak że punkt ten obraca się wraz z danym kołem.
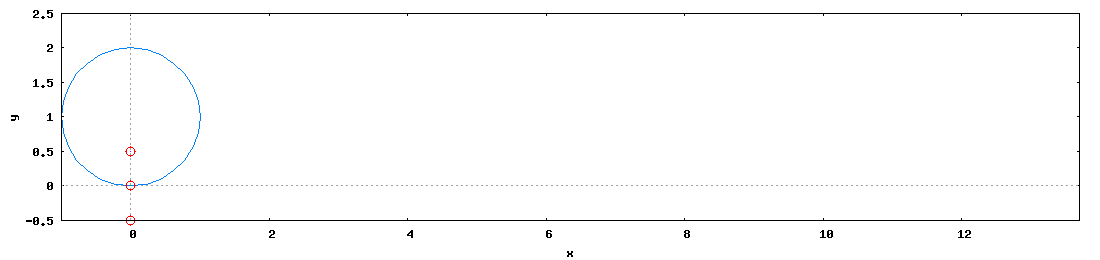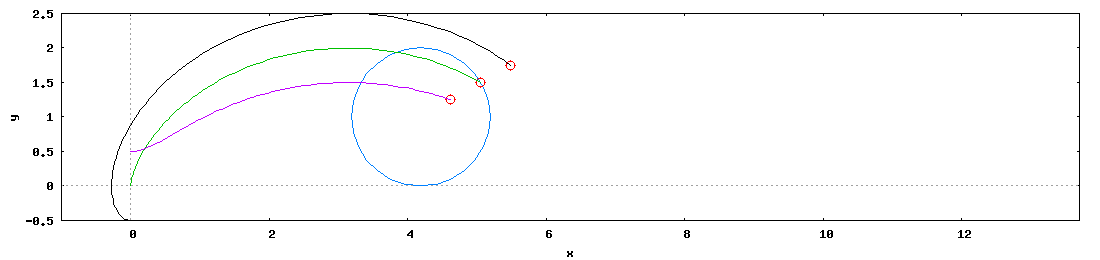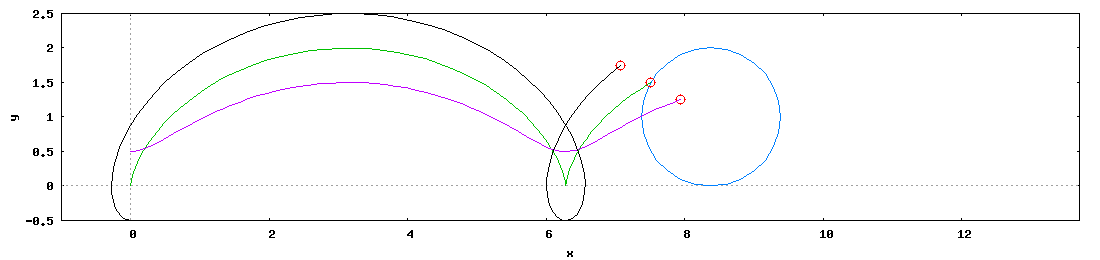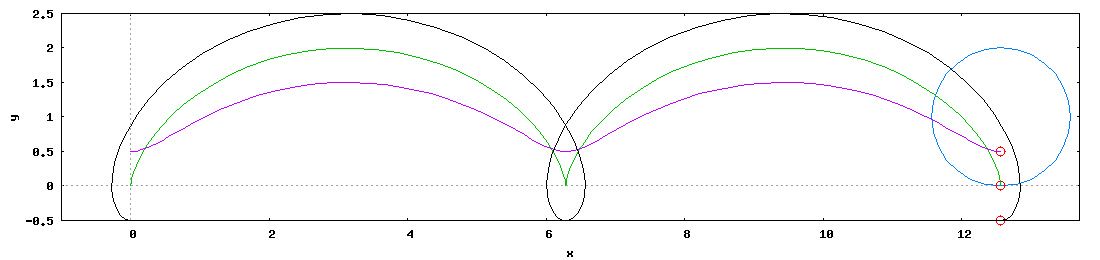
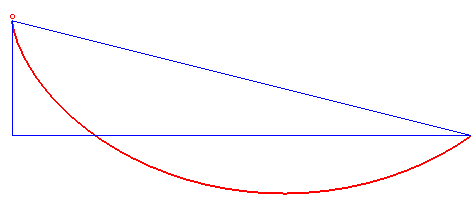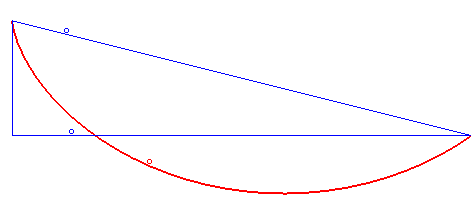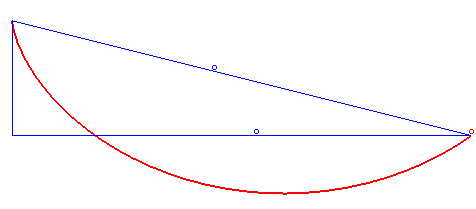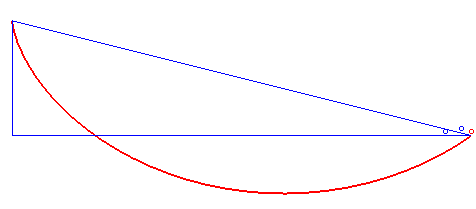
Dla ścisłości i jasności sytuacji warto łaskawym okiem zerknąć na poniższą wykreso-animację, by zrozumieć o co mi naprawdę chodzi.
- Zielona - o promieniu wodzącym Rw równym promieniu toczenia Rt nazywana cykloidą zwykłą;
- Czarna - o promieniu wodzącym Rw większym od promienia toczenia Rt nazywana cykloidą wydłużoną;
- Magenta - o promieniu wodzącym Rw mniejszym od promienia toczenia Rt nazywana cykloidą skróconą.
Poszczególne klatki powyższej animacji zostały wygenerowane w programie wxMaxima za pomocą następującego kodu:
Animację poskładałem w programie Gimp.
Opis parametryczny cykloidy
Cykloidy zwykłe można zapisać za pomocą następującego układu równań parametrycznych, w których współrzędne x i y zależą od promienia toczenia Rt i kąta obrotu φ.
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2111.gif) | [1] |
Zapis wyrażenia w formacie TeX-a:
Z kolei dla cykloid o promieniu wodzenia Rw różnym od promienia toczenia Rt równania parametryczne wyglądają następująco:
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2112.gif) | [2] |
Zapis wyrażenia w formacie TeX-a:
Długość łuku cykloidy zwykłej
Wzór na długość łuku cykloidy w zakresie kąta φ od 0 do 2·π można obliczyć za pomocą następującego wzoru:
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2113.gif) | [3] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- φ1 - kąt początkowy obrotu koła zwierający się w przedziale od 0 do 2·π radianów;
- φ2 - kąt końcowy obrotu koła zwierający się w przedziale od 0 do 2·π.
Kąty φ1 i φ2 powinny spełniać następującą nierówność: φ1<φ2.
Cykloida - zastosowanie
W obróbce skrawaniem, narzędzia skrawające wykonują ruch, który można opisać za pomocą cykloidy (najczęściej wydłużonych). Taką trajektorię ruchu mają narzędzia skrawające frezarki np. frezy palcowe, czołowe, głowice frezerskie ale również szlifierki czołowe. Istnieją programy, które służą do generowania symulowanej powierzchni uzyskanej za pomocą danej obróbki technologicznej przy zastosowaniu różnych parametrów obróbki (posuw narzędzia skrawającego, prędkość obrotowa, liczba ostrzy skrawających lub średnia gęstość upakowania ziaren ściernicy szlifującej przypadająca na jednostkę powierzchni ściernicy).
W fizyce cykloidy mają wiele wspólnego z krzywą najkrótszego czasu zwaną również Brachistochrona, której trajektoria odpowiada wycinkowi łuku krzywej cyklometrycznej.
Grafika żółwia - kreślenie cykloidy
W Pythonie znajduje się moduł turtle, który umożliwia kreślenie dwuwymiarowych krzywych. Oto kod programu, który wykreśli wycinek cykloidy:
Więcej na temat pisania programów w Pythonie oraz na temat grafiki żółwia można poczytać na stronie Programowanie → Podstawy Pythona → Grafika żółwia.