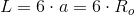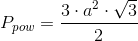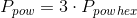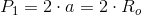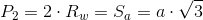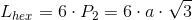Sześciokąt foremny i heksagram
Stronę tą wyświetlono już: 48777 razy
Podstawowe cechy
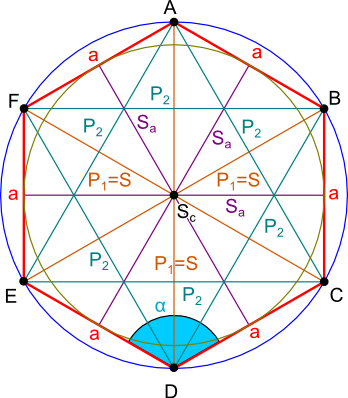
Długość boku a każdego sześciokąta foremnego jest równa promieniowi Ro okręgu opisanego na tym sześciokącie. Z kolei długość promieniaRo pomnożona przez dwa jest równa długości przekątnej głównej P1, która równocześnie jest symetralną kąta wewnętrznego α sześciokąta foremnego. Kąt α jest równy 120°. Całkowita suma kątów wewnętrznych sześciokąta foremnego wynosi 720° czyli 4·π. W sześciokącie foremnym znajdują się trzy przekątne główne P1 i sześć przekątnych krótszych P2, przy czym te ostatnie tworzą heksagram. Każdy sześciokąt foremny można podzielić na sześć trójkątów równobocznych, co stanowi podstawę wyprowadzenia wzoru na jego pole powierzchni.
Opis oznaczeń:
- A, B, C, D, E, F - wierzchołki sześciokąta foremnego;
- Sc - środek ciężkości, środek okręgu opisanego na i wpisanego w sześciokąt foremny oraz punkt przecięcia się symetralnych boków i kątów sześciokąta foremnego;
- a - boki sześciokąta foremnego;
- P1 - przekątne główne sześciokąta foremnego;
- P2 - przekątne krótsze sześciokąta foremnego;
- S - symetralne kątów wewnętrznych sześciokąta foremnego;
- Sa - symetralne boków a sześciokąta foremnego;
- α - kąt wewnętrzny sześciokąta foremnego
Jeżeli chodzi o sam hezagram, jego pole powierzchni jest równe 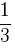 pola powierzchni sześciokąta zbudowanego na jego zewnętrznych wierzchołkach.
pola powierzchni sześciokąta zbudowanego na jego zewnętrznych wierzchołkach.
Opis oznaczeń:
- A, B, C, D, E, F - wierzchołki zewnętrzne sześciokąta foremnego i hexagramy;
- G, H, I, J, K, L - wierzchołki zewnętrzne sześciokąta foremnego i hexagramy;
- Sc - środek ciężkości, środek okręgu opisanego na i wpisanego w sześciokąt foremny oraz punkt przecięcia się symetralnych boków i kątów sześciokąta foremnego i hexagramu;
- a - boki sześciokąta foremnego;
- P2 - przekątne krótsze sześciokąta foremnego a zarazem boki hexagramu;
Podstawowe wzory
Sześciokąta foremnego
Obwód sześciokąta foremnego:
Pole powierzchni sześciokąta foremnego, gdy znana jest długość boku a a tym samym promień Ro okręgu opisanego na nim jest równe:
Znając pole powierzchni hexagramu pole powierzchni sześciokąta foremnego jest równe:
Długość przekątnej głównej P1 wynosi:
Długość przekątnej krótszej P2 wynosi:
Hexagramu
Obwód, gdy znana jest długość boku P2 hexagramu a zarazem długość krótszej przekątnej sześciokąta na nim opisanego:
Pole powierzchni hexagramu to 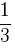 pola powierzchni sześciokąta na nim opisanego, a więc:
pola powierzchni sześciokąta na nim opisanego, a więc:
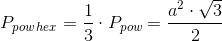 | [7] |
Zapis wyrażenia w formacie TeX-a:
Grafika żółwia - kreślenie sześciokąta i hexagramu
W Pythonie znajduje się specjalny moduł turtle poświęcony grafice żółwia, poniżej zamieszczam przykład kodu, który rysuje sześciokąt foremny:
Nic nie stoi na przeszkodzie, aby wykreślić heksagram za pomocą kodu następującego:
Na koniec rysowanie sześciokąta foremnego z heksagramem:
Więcej na temat pisania programów w Pythonie oraz na temat grafiki żółwia można poczytać na stronie Programowanie → Podstawy Pythona → Grafika żółwia.