Funkcje zależności przemieszczenia, prędkości i przyspieszenia w różnych układach odniesienia
Stronę tą wyświetlono już: 6913 razy
Na poprzedniej stronie omawiane były zagadnienia, które były wstępem do tego, o czym teraz będzie mowa. Otóż okazuje się, że dysponując wzorami określającymi zależności przemieszczenia jednej wielkości w danym układzie odniesienia od drugiej umożliwia dość łatwe wyznaczanie ogólnych wzorów dla przemieszczeń po czasie a stąd już niedaleko do wzoru na prędkość chwilową i przyspieszenie chwilowe (wystarczy pochodne po czasie wyliczyć). Co by za dużo nie biadolić zacznijmy zabawę od nawiązania do zadanie 1 z strony Fizyka → Kinematyka → Funkcje zależności położenia w różnych układach odniesienia.
Zadanie 1
Obliczyć prędkość wypadkową noża tokarskiego, który zamocowany jest na suporcie poprzecznym tokarki sprzężonym z liniałem sinusoidalnym biegnącym pod kątem α=5°, wiedząc że prędkość liniowa przenoszona na support wzdłużny tokarki jest równa Vx=5[mm/s] a funkcja opisująca położenie poprzeczne y w zależności od położenia wzdłużnego x przyjmuje postać: y(x)=tan(α)·x-20.
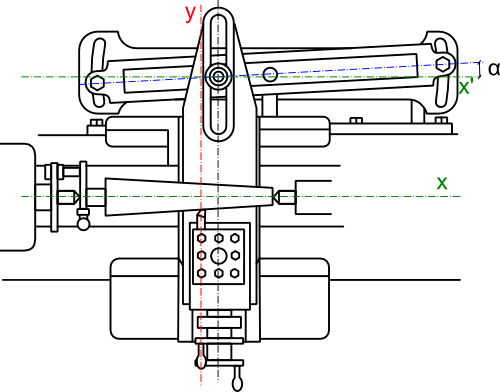
Najpierw obliczmy drogę po czasie dla kierunki x:
Teraz do wzoru na y(x) podstawić trzeba x(t) otrzymując funkcję y(t):
Policzmy prędkość liniową na kierunku y obliczając pochodną po czasie z funkcji y(t):
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2375.gif) | [3] |
Zapis wyrażenia w formacie TeX-a:
Pozostało już tylko obliczenie całkowitej prędkości chwilowej wykorzystując stare dobre twierdzenie Pitagorasa:
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2376.gif) | [4] |
Zapis wyrażenia w formacie TeX-a:
Pozostało mi tylko określenie kąta wektora, ale tak się fajnie składa, że w tym przypadku ten kąt jest nam dany i wynosi α = 5°.
Zadanie 2
Wyznacz wzór na prędkość liniową punktów A i B okręgu toczącego się bez poślizgu po płaskiej powierzchni, wiedząc że prędkość kątowa tego okręgu wynosi ω=2·π·t. Dane są funkcje zależności położenia punktów A i B od przemieszczenia kątowego φ:
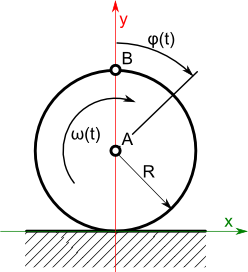
Wyznaczenie wzoru na przemieszczenie kątowe φ(t):
Podstawienie wzoru [9] do zależności [5], [6], [7] i [8]:
Obliczanie prędkości po czasie:
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_2388.gif) | [16] |
Zapis wyrażenia w formacie TeX-a:
Wartość wektora prędkości dla punktu B:
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_2390.gif) | [18] |
Zapis wyrażenia w formacie TeX-a:
Pozostało już tylko rozprawić się z zależnością przyspieszenia po czasie dla punktu A i B, które uzyskane zostaną poprzez obliczenie pochodnych po czasie zależności od [14] do [17]:
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_2394.gif) | [22] |
Zapis wyrażenia w formacie TeX-a:
Wartość wektora przyspieszenia będzie równa:
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_2395.gif) | [23] |
Zapis wyrażenia w formacie TeX-a:
Kąt wektora prędkości VB dla VBy≥0:
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_2396.gif) | [24] |
Zapis wyrażenia w formacie TeX-a:
Kąt wektora prędkości VB dla VBy<0:
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_2397.gif) | [25] |
Zapis wyrażenia w formacie TeX-a:
Kąt wektora przyspieszenia aB dla aBy≥0:
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_2398.gif) | [26] |
Zapis wyrażenia w formacie TeX-a:
Kąt wektora przyspieszenia aB dla aBy<0:
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_2399.gif) | [27] |
Zapis wyrażenia w formacie TeX-a:
Rzućmy jeszcze łaskawym okiem na wykresy funkcji Vx(t), Vy(t) i V(t) dla punktu B.
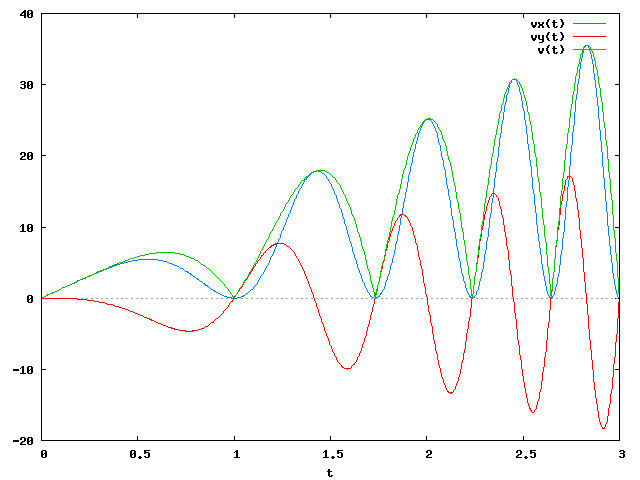
Wykres wygenerowany w programie wxMaxima za pomocą następującego polecenia:
Cóż takiego możemy powiedzieć o funkcji vx(t)? Otóż funkcja ta jest równa zero dla każdego 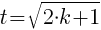 oraz dla t=0, gdzie k∈N (przez zbiór liczb naturalnych mam namyśli również 0). Innymi słowy, dla wszystkich t będących liczbami nieparzystymi Vx(t)=0. Jak mi nie wierzycie, to złapcie za kalkulator i sprawdźcie mnie bo mogę kłamać jak Tusk mówiąc o obniżaniu podatków.
oraz dla t=0, gdzie k∈N (przez zbiór liczb naturalnych mam namyśli również 0). Innymi słowy, dla wszystkich t będących liczbami nieparzystymi Vx(t)=0. Jak mi nie wierzycie, to złapcie za kalkulator i sprawdźcie mnie bo mogę kłamać jak Tusk mówiąc o obniżaniu podatków.
To jeszcze nie koniec zabawy z funkcją vx(t) albowiem warto wspomnieć, dla jakich wartości t funkcja będzie osiągała maksimum lokalne, a będzie to dla wartości 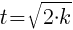 oraz
oraz 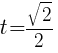 , gdzie k∈N{0}.
, gdzie k∈N{0}.
Teraz parę ciekawostek dotyczących funkcji vx(t), gdy funkcja ta jest równa zero to kąt obrotu okręgu względem jego środka jest równy φ(t)=k·pi (czyli 180°·k), gdzie k∈N a to oznacza, że wypadkowa prędkość jest równa zero, gdy punkt B dotyka powierzchni, po której okrąg się toczy.
Z kolei gdy funkcja vx(t) osiąga maksimum lokalne to kąt φ(t)=k·2·pi (czyli k·360°) dla k∈N{0} co oznacza, że punkt B w takim przypadku znajduje się w pozycji początkowej względem punktu A.
Podobną analizę można przeprowadzić dla funkcji Vy(t) oraz V(t), ale ja już tego nie będę robił pozostawiając tym samym rozwiązanie tych tajemniczych zagadnień czytelnikowi.
Podobnie można przeanalizować również funkcje ax(t), ay(t) oraz a(t), które pokazane zostały na rysunku 4.
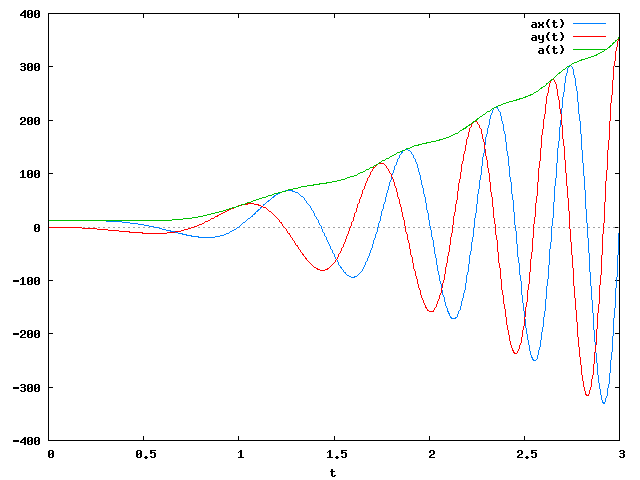
Wykres wygenerowany w programie wxMaxima za pomocą następującego polecenia:
Zadanie 3
Wyznaczyć funkcje: trajektorii ruchu, prędkości i przyspieszenia dla punktu, który porusza się po funkcji danej następującym równaniem ruchu:
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_2400.gif) | [28] |
Zapis wyrażenia w formacie TeX-a:
Wyznaczm funkcje prędkości obliczając pochodną po czasie:
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_2401.gif) | [29] |
Zapis wyrażenia w formacie TeX-a:
Teraz funkcja przyspieszenia po czasie jako pochodna funkcji prędkości po czasie:
Pozostało już tylko wyznaczyć funkcję y(x) opisującą trajektorię ruchu. Nasza funkcja y(x) jest równa 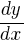 z kolei
z kolei 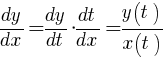 . W ostateczności więc mamy do rozważenia następujące proste równanie różniczkowe:
. W ostateczności więc mamy do rozważenia następujące proste równanie różniczkowe:
![Równanie [31]](https://obliczeniowo.com.pl/rownania/w_2403.gif) | [31] |
Zapis wyrażenia w formacie TeX-a:
Do równania [30] a w zasadzie do jego ostatecznego członu należy podstawić x(t)=7·t+14·t2 a za y(t)=4·t+8·t2.
![Równanie [32]](https://obliczeniowo.com.pl/rownania/w_2404.gif) | [32] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 4
Wyznaczyć trajektorię ruchu oraz funkcje prędkości i przyspieszenia dla następującego równania ruchu:
Wyznaczymy najpierw funkcję y(x) opisującą trajektorię ruchu naszego punktu korzystając z równania [30]:
Trzeba sobie uzmysłowić, że x(t)=x a więc 2·t2=x co po podstawieniu do równania [34] daje następującą zależność:
Wyznaczmy funkcję prędkości obliczając pochodną przemieszczenia po czasie:
oraz funkcję przyspieszenia obliczając pochodną funkcji prędkości po czasie:
Zadanie 5
Wyznaczyć trajektorię ruchu i funkcje prędkości i przyspieszenia punktu dla następującego równania ruchu:
![Równanie [38]](https://obliczeniowo.com.pl/rownania/w_2410.gif) | [38] |
Zapis wyrażenia w formacie TeX-a:
Korzystając z zależności [31] wyznaczyć należy wzór na trajektorię ruchu:
![Równanie [39]](https://obliczeniowo.com.pl/rownania/w_2411.gif) | [39] |
Zapis wyrażenia w formacie TeX-a:
Funkcja prędkości po czasie:
![Równanie [40]](https://obliczeniowo.com.pl/rownania/w_2412.gif) | [40] |
Zapis wyrażenia w formacie TeX-a:
Funkcja przyspieszenia po czasie:
![Równanie [41]](https://obliczeniowo.com.pl/rownania/w_2413.gif) | [41] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 6
Ruch punktu względem czasu opisuje następujące równanie:
![Równanie [42]](https://obliczeniowo.com.pl/rownania/w_2414.gif) | [42] |
Zapis wyrażenia w formacie TeX-a:
Wyznaczyć trajektorię ruchu oraz równania prędkości i przyspieszenia.
Trajektorię ruchu w tym przypadku opisują współrzędne walcowe:
Powyższe zależności można rozpisać dla współrzędnych walcowych w trójwymiarowym układzie w zależności od kąta φ (funkcje parametryczne):
![Równanie [46]](https://obliczeniowo.com.pl/rownania/w_2418.gif) | [46] |
Zapis wyrażenia w formacie TeX-a:
Wyznaczanie funkcji prędkości jako pochodnej po czasie funkcji przemieszczenia:
![Równanie [47]](https://obliczeniowo.com.pl/rownania/w_2419.gif) | [47] |
Zapis wyrażenia w formacie TeX-a:
Wyznaczanie funkcji przyspieszenia jako pochodnej po czasie funkcji prędkości:
![Równanie [48]](https://obliczeniowo.com.pl/rownania/w_2420.gif) | [48] |
Zapis wyrażenia w formacie TeX-a:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2373.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2374.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2377.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2378.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_2379.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_2380.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_2381.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_2382.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_2383.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_2384.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_2385.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_2386.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_2387.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_2389.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_2391.gif)
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_2392.gif)
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_2393.gif)
![Równanie [30]](https://obliczeniowo.com.pl/rownania/w_2402.gif)
![Równanie [33]](https://obliczeniowo.com.pl/rownania/w_2405.gif)
![Równanie [34]](https://obliczeniowo.com.pl/rownania/w_2406.gif)
![Równanie [35]](https://obliczeniowo.com.pl/rownania/w_2407.gif)
![Równanie [36]](https://obliczeniowo.com.pl/rownania/w_2408.gif)
![Równanie [37]](https://obliczeniowo.com.pl/rownania/w_2409.gif)
![Równanie [43]](https://obliczeniowo.com.pl/rownania/w_2415.gif)
![Równanie [44]](https://obliczeniowo.com.pl/rownania/w_2416.gif)
![Równanie [45]](https://obliczeniowo.com.pl/rownania/w_2417.gif)
