Wyznaczanie prostej prostopadłej do płaszczyzny alfa danej trzema punktami
Stronę tą wyświetlono już: 9181 razy
Znaleźć prostą prostopadłą do płaszczyzny α danej punktami A, B oraz C jak na rysunku 1, która przechodzi przez punt A płaszczyzny α.
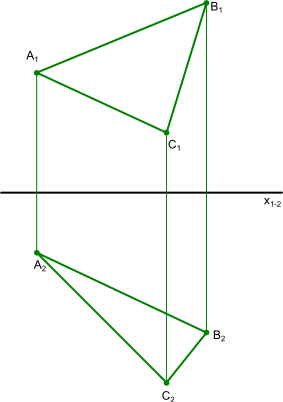
Do wyznaczenia upragnionej prostej wystarczy znaleźć linie przecięcia się płaszczyzny α z rzutniami, okazuje się bowiem, że każda prosta leżąca na danej płaszczyźnie, która jest równoległa do osi rzutni (w tym przypadku x1-2) na jednej z rzutni na drugiej płaszczyźnie rzutni jej ślad jest prostopadły do każdej prostej prostopadłej do danej płaszczyzny.
Nie będę się tutaj bawił w tłumaczenie, jak znaleźć linie przecięcia się płaszczyzny α z rzutniami π1 oraz π2 ponieważ zostało to już omówione na stronie tutaj. Dodam tylko od siebie, że w tym przypadku dane są trzy linie wyznaczające płaszczyzną α a nie dwie tak jak to miało miejsce w omawianym na wcześniej wspomnianej stronie przykładzie.
Skoro już wiadomo, że ślady S1 i S2 są prostopadłe do prostej prostopadłej do linii l1 oraz l2 to wystarczy geometrycznie za pomocą cyrkla i linijki wyznaczyć taką prostą wychodzącą z punktów A1 i A2

