Wyznaczanie linii przecięcia płaszczyzny z rzutniami danej dwiema prostymi
Stronę tą wyświetlono już: 12966 razy
Dana jest płaszczyzna α, którą wyznaczają dwie proste k oraz l. Zadaniem jest znalezienie linii przecięcia się płaszczyzny α z rzutniami π1, π2.
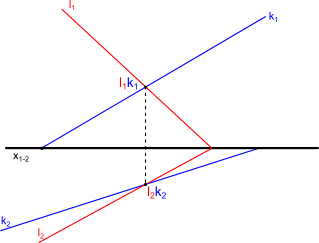
Rozwiązanie tego zadania wymaga odpowiedzenia sobie na jedno proste pytanie: kiedy ślady prostych k i l przecinają się z rzutniami?
Odpowiedź na powyższe pytanie jest następująca: ponieważ rzutnie są płaszczyznami zawsze prostopadłymi do siebie, więc gdy ślad danej linii l1 przecina się z osią rzutni na płaszczyźnie π1 to rzut tego punktu na ślad linii l2 znajdującej się na rzutni π2 wyznacza punkt przebicia tej płaszczyzny rzutni π2 z linią l.
Znając powyższą zasadę trzeba znaleźć po dwa punkty przebicia dla każdej z rzutni a następnie połączyć uzyskane punkty otrzymując tym samym linie przecięcia się płaszczyzny α z rzutniami π1 oraz π2
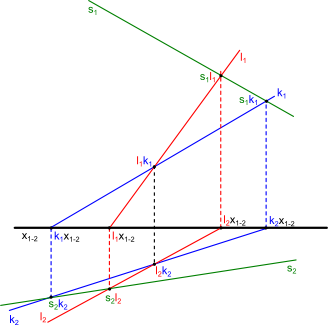
Przyjrzyjmy się teraz rysunkowi 1, na którym widać, że ślady linii l mają wspólny punkt przecięcia się z osią x1-2, a to z kolei oznacza, że już na samym początku podany jest jak na tacy punkt przecięcia się płaszczyzny α z obiema rzutniami. Z tego powodu pozostaje znaleźć tylko dwa punkty - po jednym na każdej z rzutni, aby możliwe było wyznaczenie linii przecięcia się płaszczyzny α z rzutniami. Punkty te zostaną wyznaczone poprzez zrzutowanie punktu przecięcia się śladu k2 z osią x1-2 na ślad k1 i na odwrót. Gotowe rozwiązanie zadania można zobaczyć na rysunku 2.
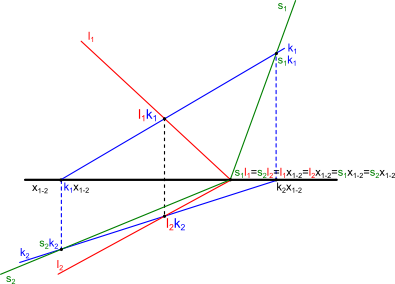
Na rysunku 3 zamieszczam nieco trudniejszą wersję zadania o tej samej treści. Jedyną różnicą w tym przypadku jest sam fakt, że żaden z śladów nie ma wspólnego punktu przecięcia z osią rzutni x1-2.
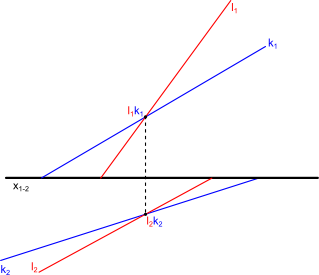
Nie tłumacząc zbyt wiele, bo w tym przypadku po prostu trzeba wyznaczyć tak jak poprzednio po dwa punkty dla śladów linii l i k na płaszczyznach rzutni, co zostało pokazane na rysunku 4.
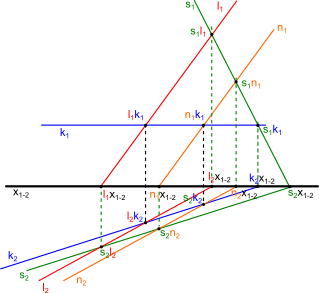
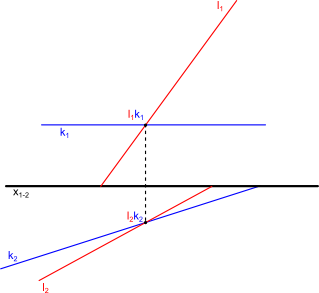
Na deser niczym wisienkę na torcie pozwoliłem sobie zostawić najtrudniejszą wersję tego zadania, w której to jeden z śladów linii jest równoległy do osi x1-2 a co za tym idzie nie da się znaleźć jego punktu przecięcia z osią x1-2. Poniżej zamieszczam rysunek tej wersji zadania.
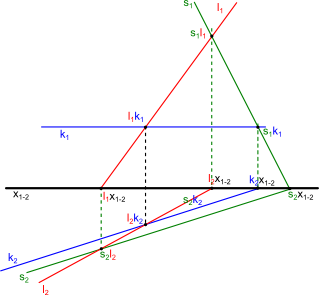
Na początek można znaleźć w konwencjonalny sposób trzy punkty stosując wcześniej omówione sztuczki co pokazane zostało na rysunku 6, ale na tym samym rysunku naniosłem obydwie linie przecięcia nieszczęsnej płaszczyzny α z rzutniami π1 i π2. Skąd wiedziałem jak poprowadzić linię s2? Odpowiedź jest prosta, linie przecięcia płaszczyzny α z rzutniami π1, π2 mają zawsze jeden punkt wspólny. Innymi słowy punkt przecięcia linii s1 z osią x1-2 jest równocześnie punktem przecięcia się linii s2 z tą osią.
Na koniec muszę dodać, że linia s1 biegnie w tym przypadku pod takim kątem, że mogłem sobie pozwolić na uproszczenie tego zadania. Są jednak przypadki, że linia ta może biegnąć pod bardzo ostrym kontem w stosunku do osi rzutni x1-2 a wtedy nie da się tak łatwo wyznaczyć linii przecięcia z tą osią. W takim przypadku na śladzie linii k1 należy wybrać sobie jeden dowolny punkt n1k1 przez który poprowadzić należy ślad linii pomocniczej n1 równoległej do śladu l1. Punkt n1k1 zrzutować należy na ślad k2 uzyskując punkt n2k2, przez który poprowadzić należy ślad linii pomocniczej n2 równoległy tym razem do śladu l2. Teraz już w standardowy sposób można wyznaczyć dodatkowy punkt s2n2 przez który przechodzi linia s2.