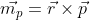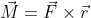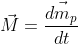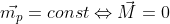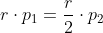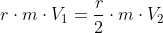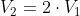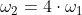Moment pędu punktu materialnego i zasada zachowania momentu pędu
Stronę tą wyświetlono już: 8970 razy
Moment pędu 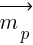 jest iloczynem wektorowym wektora promienia
jest iloczynem wektorowym wektora promienia 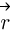 i pędu
i pędu 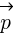 :
:
Dla lepszego zrozumienia, wektor momentu pędu 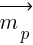 jest wektorem prostopadłym do płaszczyzny wyznaczonej przez wektor promienia
jest wektorem prostopadłym do płaszczyzny wyznaczonej przez wektor promienia 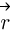 i pędu
i pędu 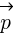 , co pokazane zostało na rysunku 1.
, co pokazane zostało na rysunku 1.
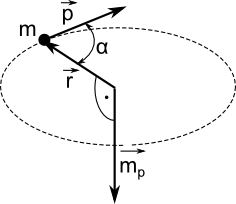
Długość wektora momentu pędu 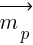 jest równa iloczynowi długości wektora promienia
jest równa iloczynowi długości wektora promienia 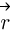 , pędu
, pędu 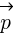 oraz sinusa kąta α zawartego pomiędzy tymi wektorami.
oraz sinusa kąta α zawartego pomiędzy tymi wektorami.
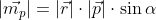 | [2] |
Zapis wyrażenia w formacie TeX-a:
W szczególnym przypadku, który mimo wszystko dość często jest rozpatrywany kąt α jest równy 90° a więc zależność [2] upraszcza się wtedy do iloczynu długości wektorów promienia 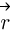 oraz pędu
oraz pędu 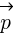 :
:
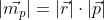 | [3] |
Zapis wyrażenia w formacie TeX-a:
Zanim zacznę opowiadać tutaj o zasadzie zachowania pędu i abyście mogli zrozumieć tę zasadę, muszę omówić najpierw pojęcie momentu siły 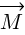 , który jest równy iloczynowi skalarnemu wektora promienia
, który jest równy iloczynowi skalarnemu wektora promienia 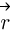 i siły
i siły 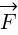 .
.
Tak jak w przypadku momentu pędu 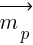 tak i w przypadku momentu siły
tak i w przypadku momentu siły 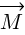 wartość skalarna jest dana następującą zależnością:
wartość skalarna jest dana następującą zależnością:
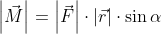 | [5] |
Zapis wyrażenia w formacie TeX-a:
I znów, tak jak w przypadku momentu pędu 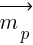 tak i w przypadku momentu siły
tak i w przypadku momentu siły 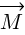 wyrażenie [5] upraszcza się, gdy kąt α jest równy 90°:
wyrażenie [5] upraszcza się, gdy kąt α jest równy 90°:
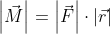 | [6] |
Zapis wyrażenia w formacie TeX-a:
Skutkiem działania momentu siły 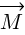 jest zmiana momentu pędu
jest zmiana momentu pędu 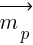 , pędu
, pędu 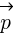 ciała jak również prędkości obwodowej
ciała jak również prędkości obwodowej 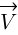 oraz kątowej
oraz kątowej 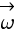 . Ponadto można stwierdzić, że gdy siła ma ten sam zwrot i kierunek co wektor pędu
. Ponadto można stwierdzić, że gdy siła ma ten sam zwrot i kierunek co wektor pędu 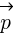 lub obwodowej prędkości chwilowej ciała
lub obwodowej prędkości chwilowej ciała 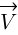 , to wektor pędu
, to wektor pędu 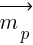 rośnie, w przeciwnym zaś przypadku maleje.
rośnie, w przeciwnym zaś przypadku maleje.
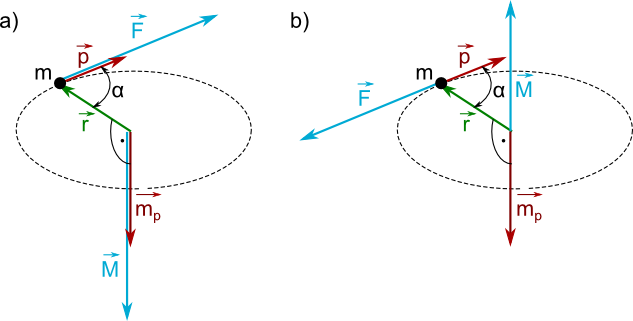
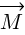 na moment pędu
na moment pędu 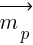 : a) gdy zwrot i kierunek wektora siły
: a) gdy zwrot i kierunek wektora siły 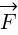 jest zgodny z kierunkiem i zwrotem wektora pędu
jest zgodny z kierunkiem i zwrotem wektora pędu 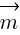 ; b) gdy zwrot wektora siły
; b) gdy zwrot wektora siły 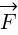 jest przeciwny do wektora pędu
jest przeciwny do wektora pędu 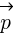 .
.Zmiana pędu po czasie 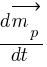 jest równa momentowi siły
jest równa momentowi siły 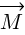 , ponieważ to siła
, ponieważ to siła 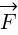 powoduje zmianę ruchu a miarą ruchu jest pęd
powoduje zmianę ruchu a miarą ruchu jest pęd 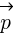 , z którym związany jest moment pędu
, z którym związany jest moment pędu 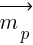 .
.
Każdy chyba się ze mną zgodzi, że już najwyższy czas aby porozmawiać o tym, znaczy się o zasadzie zachowania momentu pędu 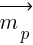 , którą w matematyczny sposób bo sposoby można zapisać tak:
, którą w matematyczny sposób bo sposoby można zapisać tak:
A po ludzku mówiąc? Po ludzku mówiąc będzie tak: jeżeli moment siły 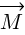 działającej na punkt materialny względem pewnego punktu w przestrzeni jest równy zeru to moment pędu
działającej na punkt materialny względem pewnego punktu w przestrzeni jest równy zeru to moment pędu 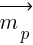 względem tego samego punktu w przestrzeni jest stały.
względem tego samego punktu w przestrzeni jest stały.
A teraz pomyślmy, przez chwilę pomyślmy logicznie i zastanówmy się kiedy moment siły 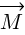 jest równy zeru? To proste, gdy siła
jest równy zeru? To proste, gdy siła 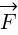 jest równa zero. A czy istnieje jeszcze jakiś przypadek, taki w którym siła
jest równa zero. A czy istnieje jeszcze jakiś przypadek, taki w którym siła 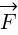 nie jest równa zeru a mimo to moment siły
nie jest równa zeru a mimo to moment siły 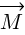 jest równy zero? Spójrzmy łaskawym okiem na wzór [5], i zastanówmy się wspólnie. Jest tam współczynnik sin α, prawda? Kiedy ten współczynnik będzie równy zero to i moment siły
jest równy zero? Spójrzmy łaskawym okiem na wzór [5], i zastanówmy się wspólnie. Jest tam współczynnik sin α, prawda? Kiedy ten współczynnik będzie równy zero to i moment siły 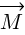 będzie równy zero. Teraz pytanie zagadka: kiedy współczynnik sin α jest równy 0? Odpowiedź brzmi, gdy α jest równe 0° lub gdy jest równe 180°. Innymi słowy, gdy kierunek siły
będzie równy zero. Teraz pytanie zagadka: kiedy współczynnik sin α jest równy 0? Odpowiedź brzmi, gdy α jest równe 0° lub gdy jest równe 180°. Innymi słowy, gdy kierunek siły 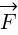 pokrywa się z kierunkiem wektora promienia
pokrywa się z kierunkiem wektora promienia 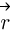 to moment siły
to moment siły 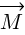 jest równy zero. Siły
jest równy zero. Siły 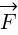 , których kierunek jest taki sam, co wektora promienia
, których kierunek jest taki sam, co wektora promienia 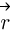 nazywa się siłami centralnymi.
nazywa się siłami centralnymi.
Skoro moment pędu 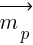 nie może ulec zmianie, bez działania na dane ciało siłą, to co się stanie, gdy zmieni się np. promień
nie może ulec zmianie, bez działania na dane ciało siłą, to co się stanie, gdy zmieni się np. promień 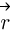 , po którym to ciało się porusza? Ponieważ promień
, po którym to ciało się porusza? Ponieważ promień 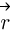 się zmniejszył, a moment pędu
się zmniejszył, a moment pędu 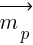 pozostał taki sam, to zmianie uległ pęd
pozostał taki sam, to zmianie uległ pęd 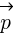 ciała. Z kolei pęd
ciała. Z kolei pęd 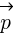 to iloczyn masy m ciała i wektora prędkości
to iloczyn masy m ciała i wektora prędkości 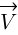 . Masa m ciała jest stała, więc pozostaje tylko się domyślać, że to prędkość
. Masa m ciała jest stała, więc pozostaje tylko się domyślać, że to prędkość 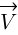 ulegnie zmianie, a skoro tak, to i prędkość kątowa ω musi ulec zmianie.
ulegnie zmianie, a skoro tak, to i prędkość kątowa ω musi ulec zmianie.
Rozważmy więc następującą sytuację: kulka zawieszona na sznurku o długości r przeplecionym przez tulejkę wprawiona została w ruch obrotowy, po czym bez działania już siłą promień ruchu kulki zmniejszono dwukrotnie. Jak zmieni się prędkość liniowa 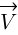 i kątowa ω?
i kątowa ω?
Z zasady zachowania pędu skorzystać należy i rozpisać następujące równanie (przyjmuję tutaj, że wektor pędy 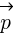 jest prostopadły do wektora promienia
jest prostopadły do wektora promienia 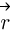 ):
):
Pęd p jest równy iloczynowi masy m i prędkości V, więc równanie [9] można jeszcze troszeczkę rozpisać:
Po odpowiednim przekształceniu i uproszczeniu równania [10] otrzymuje się prędkość liniową V2 po zmniejszeniu promienia r o połowę.
Prędkość liniowa wzrosła dwukrotnie, a kątowa ω ile razy? Na to dręczące nas pytanie można odpowiedzieć jedynie stosując wzór na prędkość kątową ω w zależności od prędkości obwodowej V zastosowane w równaniu [10]:
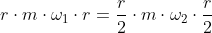 | [12] |
Zapis wyrażenia w formacie TeX-a:
Przekształcając otrzymujemy:
Prędkość kątowa ω2 wzrosła czterokrotnie, a wszystko to dlatego, że promień r zmalał dwukrotnie.
Zasada zachowania momentu pędu 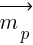 ma również zastosowanie w przypadku ruchu Księżyca wokół Ziemi (jak również innych ciał niebieskich).
ma również zastosowanie w przypadku ruchu Księżyca wokół Ziemi (jak również innych ciał niebieskich).