Twierdzenie Pitagorasa
Stronę tą wyświetlono już: 12953 razy
Różne sposoby udowadniania słuszności twierdzenia Pitagorasa
Kto nie zna twierdzenia Pitagorasa, ten zapewne nie skończył jeszcze szkoły podstawowej. Jest to jedno z najbardziej znanych twierdzeń, którego powstanie przypisuje się Pitagorasowi żyjącemu w latach około 580 - 500 p.n.e. W książce Śladami Pitagorasa autorstwa Szczepana Jeleńskiego na stronie 18 można przeczytać nad podobnym rysunkiem do rysunku 1 taki oto tekst: "A oto przypuszczalny dowód Pitagorasa:"
Z rysunku 1 można jednoznacznie odczytać, że kwadraty po lewej jak i po prawej stronie mają takie same długości boków równe sumie długości przyprostokątnych a i b trójkątów prostokątnych wrysowanych w te kwadraty. Kwadrat po prawej stronie składa się z czterech takich samych trójkątów prostokątnych i jednego kwadratu o boku c i polu powierzchni c2, natomiast kwadrat po prawej stronie składa się z czterech tych samych trójkątów oraz dwóch kwadratów o bokach a i b. Wniosek nasuwa się samemu, skoro oba duże kwadraty mają takie same pola powierzchni a po odjęciu od nich pól powierzchni czterech trójkątów otrzymuje się pola równe c2 dla lewego kwadratu z rysunku 1 i a2, b2 dla kwadratu drugiego to prawdziwa jest następująca równość:
Czyli, ubierając wzór [1] w słowa: kwadrat długości najdłuższego boku trójkąta prostokątnego jest równy sumie kwadratów długości pozostałych boków tego trójkąta.
Dla części lewej rysunku 1 prawdziwa jest równość:
Dla części prawej rysunku 1 prawdziwa jest natomiast następująca równość:
Ponieważ lewe strony równań [2] i [3] są takie same, więc ich prawe strony muszą się sobie równać, a więc ostateczne zdanie matematyczne potwierdzające prawdziwość twierdzenia Pitagorasa jest następujące:
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_729.gif) | [4] |
Zapis wyrażenia w formacie TeX-a:
Tak naprawdę do udowodnienia twierdzenia Pitagorasa wystarczy lewa część rysunku 1. Coby lepiej się udowadniało część lewą rysunku przerysować mi się zachciało.
Do rysunku 2 jak i do lewej części rysunku 1 napisana została zależność [2], która po rozpisaniu przyjmuje następującą postać:
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_730.gif) | [5] |
Zapis wyrażenia w formacie TeX-a:
Ale to jeszcze nie wszystko, otóż w 1876r. znalazł się taki człowiek, który stwierdził, że do udowodnienia słuszności twierdzenia Pitagorasa wystarczy mu połowa rysunku 2, a co za tym idzie 1/4 rysunku 1. Człowiekiem tym był James Garfield dwudziesty prezydent Stanów Zjednoczonych Ameryki. Zerknijmy więc łaskawym okiem na jego sposób udowodnienia twierdzenia Pitagorasa, do którego posłuży znów częściowo przerysowany rysunek 1 i 2.
Tak więc ścinając prostokąt z rysunku 1 i 2 po przekątnej kwadratu o boku c James Garfield znalazł kolejny sposób na udowodnienie twierdzenia Pitagorasa. Albowiem teraz wystarczy tylko rozpisać równanie, którego lewą stroną będzie suma wyrazów na pole powierzchni trzech trójkątów prostokątnych (patrz rysunek 3), natomiast prawą wzór na pole powierzchni trapezu na jaki się owe trójkąty składają (również patrz rysunek 3). Zgodnie z tym co już zostało napisane rozpisać należy matematyczne równanie w następujący sposób:
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_731.gif) | [6] |
Zapis wyrażenia w formacie TeX-a:
Oczywiście po odpowiednim przekształceniu dojść można do następującej postaci równania [6]:
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_732.gif) | [7] |
Zapis wyrażenia w formacie TeX-a:
Jeśli nie daje Ci spokoju odpowiedź na pytanie, czy można jeszcze bardziej zredukować część graficzną niezbędną do udowodnienia twierdzenia Pitagorasa to Musisz wiedzieć, że tak jest to możliwe, aczkolwiek tym razem konieczne będzie zastosowanie twierdzenia o równości stosunków odpowiadających sobie dwóch boków w takich trójkątach.
Tak jak już wspominałem, na mocy twierdzenia mówiącego, że dwa trójkąty są do siebie podobne, gdy ich dwa dowolne kąty są sobie równe a przypadek ten spełniają trójkąty ABC, ABD jak i BCD, a więc wszystkie te trójkąty są podobne. Zanim zastosowane zostanie drugie twierdzenie o trójkątach podobnych, zapisać należy następującą równość, dotyczącą długości trzech boków L1, L2 oraz c:
W trójkątach podobnych stosunek dwóch boków w jednym trójkącie do odpowiadających mu dwóm bokom trójkąta drugiego są sobie równe, z czego należy skorzystać i zapisać dwie nowe zależności:
Zależności [9] i [10] podstawić należy do równania [8], otrzymując następujące wyrażenie:
Czas na dowód czysto geometryczny, w którym skorzystać należy z konstrukcji geometrycznej z rysunku 5.
Podstawą dowodu, jest podział kwadratu ACHI na dwa prostokąty AIJK, CHJK oraz udowodnienie, że pole powierzchni prostokąta AIJK jest równe polu powierzchni kwadratu ABED a pole powierzchni prostokąta AIJK jest równe polu powierzchni kwadratu BCGF.
Aby udowodnić równość pola powierzchni kwadratu ABED polowi powierzchni prostokąta AIJK należy zauważyć, że wprowadzając odcinki DC oraz BI uzyskuje się dwa trójkąty ACD oraz ABI, dla których można na mocy twierdzenia o podobieństwie trójkątów mówiącego że: dwa trójkąty są przystające, gdy co najmniej dwa boki tych trójkątów są sobie równe oraz odpowiedni kąt w obu tych trójkątach jest taki sam można udowodnić, że trójkąty te są przystające. Jak widać z rysunku 5 obydwa trójkąty zawierają kąt prosty powiększony o kąt zawarty pomiędzy ramionami AB oraz AC trójkąta prostokątnego ACB, z czego wynika że mają one takie same kąty pomiędzy ramionami o wymiarach a i c.
Przyjrzyjmy się teraz bliżej trójkątowi ACD, którego wysokość spuszczona na bok DA jest równa a, a więc pole powierzchni tego trójkąta jest równe połowie pola powierzchni prostokąta ABED. I przez analogię do wcześniejszego wywodu, wysokość trójkąta ABI spuszczona na jego bok AI jest równa bokowi AK prostokąta AIJK co udowadnia niezbicie, że pole powierzchni tego trójkąta jest równe połowie pola powierzchni prostokąta AIJK.
Ponieważ trójkąty ACD i ABI są trójkątami przystającymi, muszą one mieć również takie same pola powierzchni a to w powiązaniu z wcześniejszym wywodem jest niezbitym wszak dowodem, na równość pól powierzchni kwadratu ABED oraz prostokąta AIJK.
Analogicznie należy postąpić dla prostokąta CHJK oraz kwadratu BCGF, wprowadzając odcinki AG oraz BH tworzące trójkąty podobne ACG oraz BCH. A gdy się już to zrobi, i zapomni się dlaczego się to robiło wystarczy spojrzeć łaskawym okiem jeszcze raz na rysunek 5 aby zrozumieć, że skoro suma pól powierzchni prostokąta AIJK oraz prostokąta CHJK jest równe polu powierzchni kwadratu ACHI to twierdzenie Pitagorasa jest jak najbardziej prawdziwe (innymi słowy, skubaniec nie kłamał).
Czas na dowód autorstwa Bhaskara II, słynnego matematyka hinduskiego z XII wieku, autora Lilavati słynnej książki o arytmetyce. Ponoć autor tego dowodu Pitagorasa pod rysunkiem podobnym do rysunku 6 napisał: "patrz".
Żeby nie było żadnych wątpliwości, przedstawiam rysunek 6 zapisany w matematycznym zdaniu równości:
z którego wynika niezbicie twierdzenie Pitagorasa oczywiście:
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_738.gif) | [13] |
Zapis wyrażenia w formacie TeX-a:
Powiązania mafijne twierdzenia Pitagorasa z funkcjami trygonometrycznymi - czyli jak to ludzie twierdzenie Pitagorasa przemienili w jedynkę trygonometryczną.
Dzieląc obustronnie wzór Pitagorasa przez c2 uzyskuje się następujące równanie:
Do równania [14] należy przypomnieć sobie dwa następujące podstawowe wzory trygonometryczne:
Wzory [15], [16] podstawiamy do równania [14] i jedynka trygonometryczna jest gotowa.
Dla tych, którzy nie wiedzą, za pomocą jedynki trygonometrycznej można obliczyć cos(α) gdy znany jest sin(α) i na odwrót (przydaje się niekiedy w programowaniu). Jedynka trygonometryczna używana jest niekiedy przy obliczaniu całek niektórych funkcji trygonometrycznych, np. takich jak ta:
![Równanie [18]](https://obliczeniowo.com.pl/rownania/w_743.gif) | [18] |
Zapis wyrażenia w formacie TeX-a:
Zastosowanie twierdzenie Pitagorasa do wyznaczania długości wektora oraz odległości dzielącej dwa wektory od siebie
Obliczenie długości wektora 2D jest banalnie proste, wystarczy bowiem znać składowe x, y danego wektora V, aby możliwe było obliczenie długości tego wektora według następującej zależności stanowiącej przekształcenie twierdzenia Pitagorasa:
Uzupełnieniem do równania [19] jest rysunek 7, na którym obejrzeć można graficzną interpretację wektora V wraz z jego składowymi x, y.
Umieśćmy teraz wektor V w trójwymiarowej przestrzeni, i zbudujmy na jego podstawie wektor V', którego składowa z jest większa od 0 a pozostałe składowe są równe składowymi x, y wektora V jak na rysunku 8.
Z rysunku 8 wynika następujący tok rozumowania, powstały w oparciu o stanowiące podstawę do tych wyliczeń równanie [19]:
![Równanie [20]](https://obliczeniowo.com.pl/rownania/w_745.gif) | [20] |
Zapis wyrażenia w formacie TeX-a:
Wyprowadzenie wzoru na odległość pomiędzy dwoma punktami nie stanowi żadnego problemu, wystarczy zastosować wzór [19] dla wektorów 2D w oparciu o rysunek 9.
Jak widać, na podstawie rysunku 9 i równania [19] zapisać można następujący wzór:
![Równanie [21]](https://obliczeniowo.com.pl/rownania/w_746.gif) | [21] |
Zapis wyrażenia w formacie TeX-a:
W analogiczny sposób można postąpić z wzorem [20]:
![Równanie [22]](https://obliczeniowo.com.pl/rownania/w_747.gif) | [22] |
Zapis wyrażenia w formacie TeX-a:
Osoby używające programów typu CAD do sporządzania dokumentacji technicznych powinny zdawać sobie sprawę, że wymiarując taki rysunek lub mierząc odległość jakiegoś odcinka na takim rysunku wykorzystywane jest również twierdzenie Pitagorasa.
Wzory geometryczne, wyprowadzone za pomocą twierdzenia Pitagorasa
Jakby nie spojrzeć i jakby nie patrzeć, twierdzenie Pitagorasa umożliwiło wyprowadzenie wzorów na pole powierzchni trójkąta równoramiennego oraz równobocznego. Zaczynając od trójkąta równoramiennego, na podstawie rysunku 10 możliwe jest wyprowadzenie następującego wzoru na wysokość tego typu trójkąta:
![Równanie [23]](https://obliczeniowo.com.pl/rownania/w_748.gif) | [23] |
Zapis wyrażenia w formacie TeX-a:
Stosując równanie [23] do równania ogólnego na pole powierzchni trójkąta:
uzyskuje się wzór na pole powierzchni trójkąta równoramiennego:
![Równanie [25]](https://obliczeniowo.com.pl/rownania/w_750.gif) | [25] |
Zapis wyrażenia w formacie TeX-a:
Oczywiście, gdy bok b trójkąta równoramiennego jest równy długości boku a, to równanie [24] upraszcza się do postaci wzoru na pole powierzchni trójkąta równobocznego:
Kolejną konsekwencją, wyprowadzenie równania [25] jest wyprowadzenie na jego podstawie wzoru na pole powierzchni sześciokąta foremnego na podstawie rysunku 11.
Jak wynika z rysunku 11 sześciokąt foremny można podzielić na sześć trójkątów równoramiennych, a więc pole powierzchni sześciokąta stanowi sześciokrotność pola powierzchni trójkąta równoramiennego o boku a równym długości boku danego sześciokąta foremnego (równanie [26]).
Z jednego wzoru na wysokość h trójkąta równoramiennego, uzyskanego dzięki twierdzeniu Pitagorasa można było wyprowadzić trzy wzory na pole powierzchni trzech figur geometrycznych: trójkąta równoramiennego, trójkąta równobocznego i sześciokąta foremnego. Oczywiście przykładów na zastosowanie twierdzenia Pitagorasa w geometrii obliczeniowej można mnożyć i mnożyć ale nie o to chodzi, żebym zasypywał tutaj temat stertą tysiąca, czy nawet większej ilości przykładów, a jedynie o to żeby pokazać niezbicie jego przydatność i mnogość dobrodziejstw wynikających z jego wyprowadzenia.
Mafijne powiązania Einsteinowskiej teorii względności czasu z twierdzeniem Pitagorasa
W książce Jeya Oreara pt. "Fizyka tom 1" w rozdziale 8.3 Dylatacja czasu str. 133 znajduje się opis wyprowadzenia wzoru na dylatację czasu za pomocą teoretycznej konstrukcji dwóch zegarów świetlnych: zegara A nieruchomego i zegara B poruszającego się z prędkością V jak na rysunku 12.
Zegary te są wyidealizowane, to znaczy z zwierciadłami doskonale odbijającymi światło. W chwili t = 0[s] w zegarze A oraz B wysłany został impuls świetlny, jednakże impuls ten w zegarze B patrząc z perspektywy układu odniesienia związanego z zegarem A musi przebyć dłuższą drogę równą cT. Jak wynika z rysunku 12 możliwe jest napisanie następującej równości będącej oczywiście zastosowaniem twierdzenia Pitagorasa:
![Równanie [28]](https://obliczeniowo.com.pl/rownania/w_753.gif) | [28] |
Zapis wyrażenia w formacie TeX-a:
Równanie [28] należy przekształcić wyznaczając z niego T w następujący sposób:
![Równanie [29]](https://obliczeniowo.com.pl/rownania/w_754.gif) | [29] |
Zapis wyrażenia w formacie TeX-a:
Znając upływ czasu w układzie związanym z zegarem A można obliczyć upływ czasu zaobserwowany w tymże układzie w zegarze B.
Zakończenie
Ponad dwa i pół tysiąca lat temu żył sobie człowiek, który odkrył pewną geometryczną zależność pomiędzy długościami boków trójkąta prostokątnego. Od tamtego czasu przez wieki ludzie wymyślali coraz to nowsze sposoby na udowodnienie słuszności Jego twierdzenia, jak również znajdowali zastosowanie tego twierdzenia w różnych obliczeniach geometrycznych. A gdy w 1941 roku powstała pierwsza maszyna programowalna, która dała podwaliny pod dzisiejsze komputery osobiste owo twierdzenie miało około dwóch tysięcy czterystu sześćdziesięciu lat. Dzisiejsze komputery w różnych algorytmach grafowych wykorzystują to twierdzenie, umożliwiając tym samym rozwiązanie często znacznie bardziej złożonych obliczeń czy symulacji. Żaden człowiek nie byłby w stanie w tak zażarty sposób "wykorzystać" to twierdzenie powstałe dwa i pół tysiąca lat temu tak jak robią to maszyny. Dziś już mało kto interesuje się twierdzeniem Pitagorasa, mało kto wie, że wykorzystuje je na co dzień, chociażby grając w jakąś grę, czy tworząc dokumentacje techniczne w programie CAD-owskim.
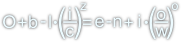
![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_726.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_727.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_728.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_733.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_734.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_735.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_736.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_737.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_739.gif)
![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_740.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_741.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_742.gif)
![Równanie [19]](https://obliczeniowo.com.pl/rownania/w_744.gif)
![Równanie [24]](https://obliczeniowo.com.pl/rownania/w_749.gif)
![Równanie [26]](https://obliczeniowo.com.pl/rownania/w_751.gif)
![Równanie [27]](https://obliczeniowo.com.pl/rownania/w_752.gif)