Obrót wektora o kąt
Stronę tą wyświetlono już: 26995 razy
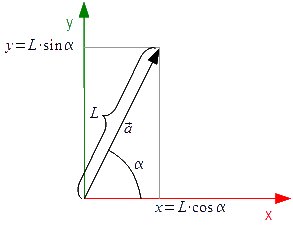
Dla danego dwuwymiarowego wektora a można zapisać następującą zależność wypadkowych x, y od długości L i kąta α:
gdzie:
- α - kąt położenia wektora a względem osi x.
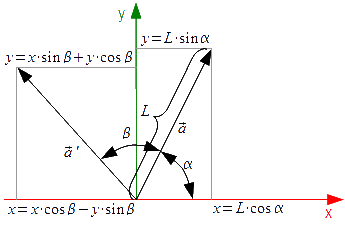
Załóżmy teraz, że obracając wektor a względem środka układu współrzędnych o zadany kąt β uzyskiwany jest wektor a'. Obrót wektora a można więc zapisać następująco:
gdzie:
- α - kąt położenia wektora a względem osi x;
- β - kąt zawarty między wektorami a, a' ;
- β+α - kąt położenia wektora a' względem osi x.
Przejście z drugiego członu równania [2] do członu trzeciego umożliwiło zastosowanie wzorów [26], [27] znajdujących się w dziale Matematyka → Funkcje → Funkcje trygonometryczne. Dzięki owym wzorom można obracać dany wektor względem początku układu współrzędnych nie martwiąc się przy tym o początkową wartość kąta położenia wektora obracanego. Stanowi to wielkie udogodnienie dla programów posługujących się grafiką wektorową (i nie tylko), wiele gier i programów graficznych wykorzystuje tą metodę chociażby do obracania bitmap, czy też dwuwymiarowych grafik wektorowych.
Istnieje również możliwość zapisu obrotu wektora 2W o zadany kąt β za pomocą mnożenia obracanego wektora a przez macierz obrotu w następujący sposób:
Przykładowy rysunek-animacja dla obrotu obiektu płaskiego względem początku układu współrzędnych znajduje się poniżej.
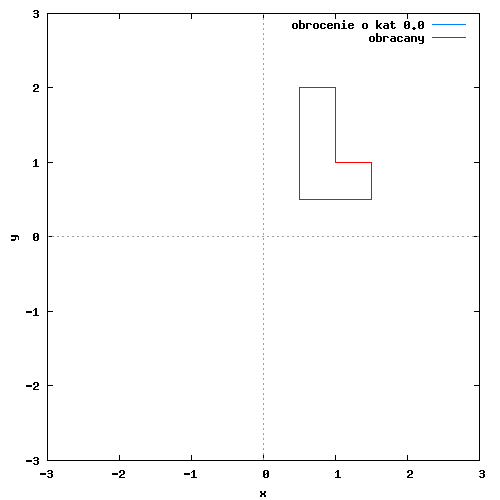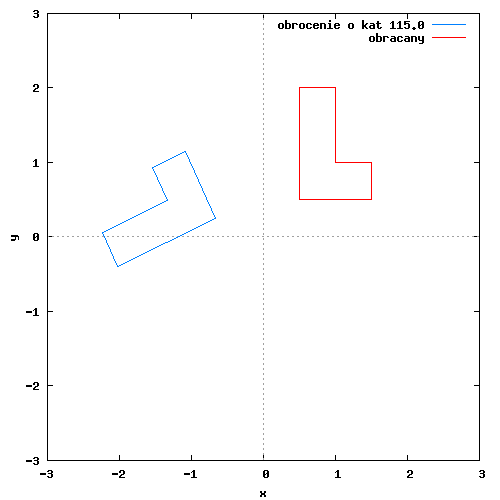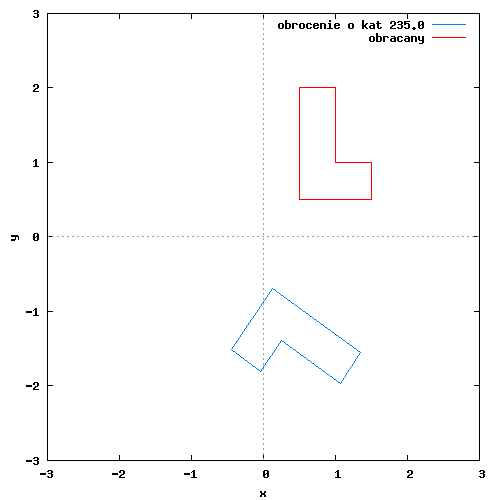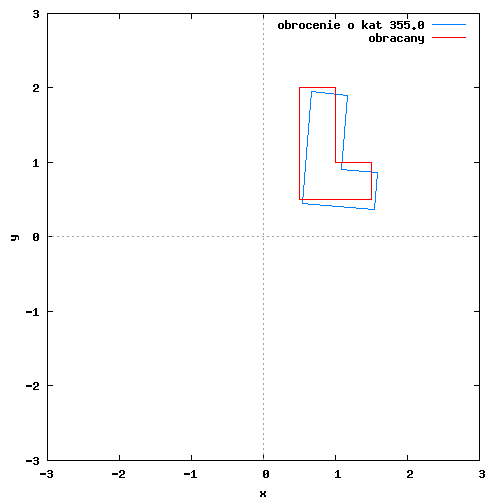
Poszczególne klatki animacji wygenerowane zostały w programie wxMaxima za pomocą następującego kodu:
Animacja poskładana w programie Gimp.
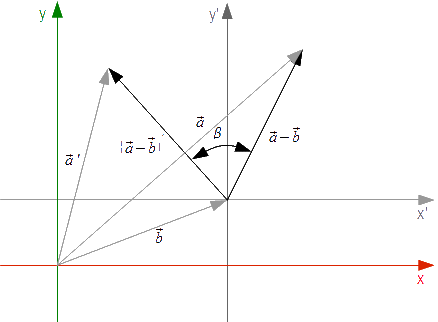
Obrót punktu a względem dowolnego punktu b można potraktować jako obrót punktu a-b względem środka układu współrzędnych z dodaniem do obróconego wektora wektora b w następujący sposób:
Dla lepszego zrozumienia warto zerknąć na rysunek 4, gdzie jak widać obrót wykonywany jest na punkcie a-b otrzymując obrócony punkt (a-b)'. W celu wyznaczenia poszukiwanego punktu a' konieczne staje się dodanie do punktu (a-b)' punktu b. W punkcie obrotu b można umieścić przesunięty układ współrzędnych x'y', który umożliwia zastosowanie wzoru [3] do obrócenia wektora (a-b) o kąt β.
Skoro obczailiśmy już obroty wektora 2W najwyższy czas już nastał aby obczaić obroty wektora 3W. Podejrzewam, że nie będzie dla nikogo wielkim zaskoczeniem gdy napiszę, że obrót wektora 2W jest pewnym uproszczeniem obrotów wektorów 3W a ściślej rzecz ujmując, jest to przypadek obrotu wektora leżącego równolegle do płaszczyzny xy względem osi z. Żeby nie przynudzać zbytnio przejdę do konkretów, czyli do wzoru na obrót wektora 3W względem osi z:
Poniżej zamieszczam animację obrotu przykładowego obiektu wokół osi z.
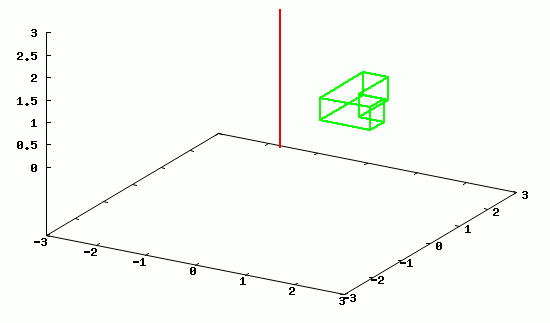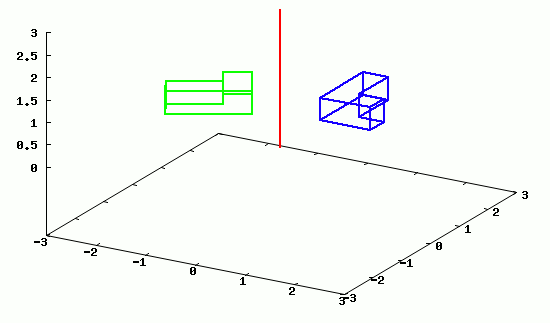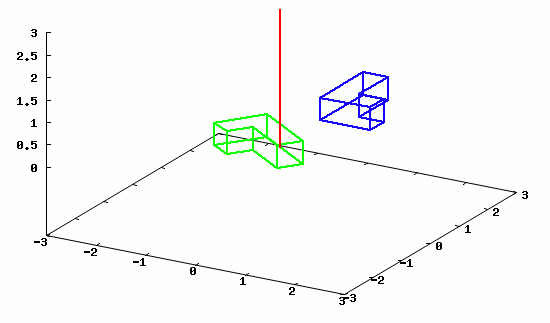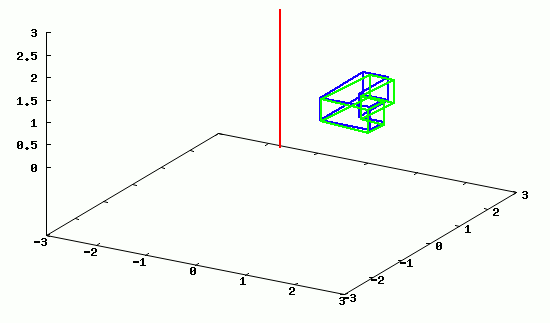
Poszczególne klatki animacji wygenerowane w programie wxMaxima
Animacja poskładana w programie Gimp
Analogiczny wzór można napisać dla obrotu punktu względem osi y:
oraz wzór na obrót względem osi x:
Możliwy jest obrót punktu a wokół osi równoległej do osi z układu współrzędnych, przechodzącej przez zadany punkt b w następujący sposób:
Jak widać we wzorze [8] pominięta została składowa bz ponieważ dla obrotu względem osi równoległej do osi z składowa bz nie wpływa na wynik obliczeń. W analogiczny sposób można zapisać wzór na obrót punktu względem osi równoległej do osi y i przechodzącej przez punkt b:
Oczywiście dla obrotu punktu a względem osi równoległej do osi x i przechodzącej przez punkt b również można zapisać następujący wzór:
Obrót punktu o kąty: 90°, 180°, 270° można zrealizować w znacznie prostszy sposób w oparciu o rysunek 4. Z owego rysunku wynika, że odpowiednie przestawienie współrzędnych wektora a z uwzględnieniem zmiany znaków umożliwia dużo łatwiejsze uzyskanie obróconego punktu. Metodę tą stosuje się w programowaniu, gdy obrót punktu w danym przypadku zawsze jest równy jednej z wymienionych wcześniej wartości kątów.
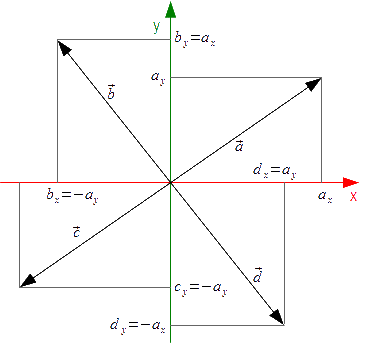
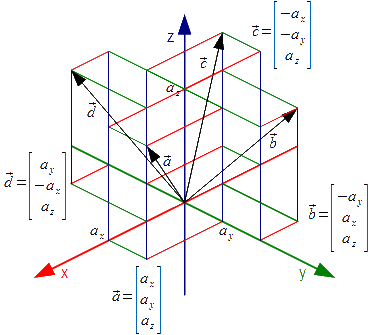
Tą samą metodą można obracać dany wektor a względem osi układu współrzędnych 3W, przykład obrotu takiego wektora względem osi z o kąty 90°, 180° oraz 270° można zobaczyć na rysunku 7.

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1108.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1109.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1110.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_1111.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_1112.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1113.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_1114.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_1115.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_1116.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_1117.gif)