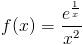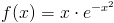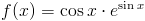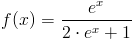Obliczanie całek funkcji wykładniczych i logarytmicznych
Autor podstrony: Krzysztof Zajączkowski
Stronę tą wyświetlono już: 4290 razy
Zadanie 1 Obliczyć całkę z funkcji:
 |
[1] |
Zapis wyrażenia w formacie TeX-a:
f(x)=ln x
Rozwiązanie:
![rozwiązanie całki z funkcji [1]](https://obliczeniowo.com.pl/rownania/w_1561.gif) |
[2] |
Zapis wyrażenia w formacie TeX-a:
\int \ln x\,dx\begin{vmatrix}
u=ln x
du=\frac{1}{x}\,dx
dv=dx
v=\int\,dx=x
\end{vmatrix}=x\cdot ln x-\int\frac{1}{x}\cdot x\,dx=x\cdot ln x-x+c
Zadanie 2 Obliczyć całkę z funkcji:
 |
[3] |
Zapis wyrażenia w formacie TeX-a:
f(x)=frac{ln^2x}{x}
Rozwiązanie:
![rozwiązanie całki z funkcji [3]](https://obliczeniowo.com.pl/rownania/w_1563.gif) |
[4] |
Zapis wyrażenia w formacie TeX-a:
\int\frac{ln^2x}{x}\,dx\begin{vmatrix}
ln x=t
\frac{dx}{x}=dt
\end{vmatrix}=\int t^2\,dt=\frac{1}{3}\cdot t^3=\frac{1}{3}\cdot ln^3x+c
Zadanie 3 Obliczyć całkę z funkcji:
 |
[5] |
Zapis wyrażenia w formacie TeX-a:
f(x)=\frac{\sqrt{2+ln x}}{x}
Rozwiązanie:
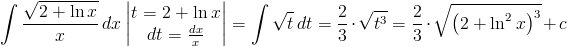 |
[6] |
Zapis wyrażenia w formacie TeX-a:
\int\frac{\sqrt{2+ln x}}{x}\,dx\begin{vmatrix}
t=2+ln x
dt=\frac{dx}{x}
\end{vmatrix}=\int\sqrt{t}\,dt=\frac{2}{3}\cdot\sqrt{t^3}=\frac{2}{3}\cdot\sqrt{\left(2+ln^2x\right)^3}+c
Zadanie 4 Obliczyć całkę z funkcji:
 |
[7] |
Zapis wyrażenia w formacie TeX-a:
f(x)=\frac{1}{x\cdot\sqrt{1-ln x}}
Rozwiązanie:
![rozwiązanie całki funkcji [7]](https://obliczeniowo.com.pl/rownania/w_1567.gif) |
[8] |
Zapis wyrażenia w formacie TeX-a:
\int\frac{dx}{x\cdot\sqrt{1-ln x}}\begin{vmatrix}
ln x=t
\frac{dx}{x}=dt
\end{vmatrix}=\int\frac{dt}{\sqrt{1-t^2}}=arcsin t=arcsin ln x+c
Zadanie 5 Obliczyć całkę z funkcji:
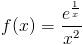 |
[9] |
Zapis wyrażenia w formacie TeX-a:
f(x)=\frac{e^\frac{1}{x}}{x^2}
Rozwiązanie:
![rozwiązanie całki z funkcji [9]](https://obliczeniowo.com.pl/rownania/w_1569.gif) |
[10] |
Zapis wyrażenia w formacie TeX-a:
\int\frac{e^\frac{1}{x}}{x^2}\,dx\begin{vmatrix}
\frac{1}{x}=t
-\frac{1}{x^2}=dt
\end{vmatrix}=-\int e^t\,dt=-e^t=-e^\frac{1}{x}+c
Zadanie 6 Obliczyć całkę z funkcji:
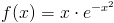 |
[11] |
Zapis wyrażenia w formacie TeX-a:
f(x)=x\cdot e^{-x^2}
Rozwiązanie:
![rozwiązanie całki z funkcji [11]](https://obliczeniowo.com.pl/rownania/w_1571.gif) |
[12] |
Zapis wyrażenia w formacie TeX-a:
\int x\cdot e^{-x^2}dx\begin{vmatrix}
-x^2+1=t
-2\cdot x\,dx=dt
dx=-\frac{dt}{2\cdot x}
\end{vmatrix}=-\frac{1}{2}\cdot\int x\cdot e^t\cdot\frac{dt}{x}=-\frac{1}{2}\cdot e^t=-\frac{1}{2}\cdot e^{-x^2}+c
Zadanie 7 Obliczyć całkę z funkcji:
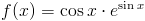 |
[13] |
Zapis wyrażenia w formacie TeX-a:
f(x)=cos x\cdot e^{sin x}
Rozwiązanie:
![rozwiązanie całki z funkcji [13]](https://obliczeniowo.com.pl/rownania/w_1573.gif) |
[14] |
Zapis wyrażenia w formacie TeX-a:
\int cos x\cdot e^{sin x}\,dx\begin{vmatrix}
t=sin x
dx=cos x\,dx
\end{vmatrix}=\int e^t\,dt=e^t=e^{sin x}+c
Zadanie 8 Obliczyć całkę z funkcji:
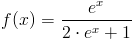 |
[15] |
Zapis wyrażenia w formacie TeX-a:
f(x)=\frac{e^\frac{1}{x}}{x^2}
Rozwiązanie:
 |
[16] |
Zapis wyrażenia w formacie TeX-a:
\int\frac{e^x}{2\cdot e^x+1}\,dx=\frac{1}{2}\cdot\int\frac{2\cdot e^x\,dx}{2\cdot e^x+1}\begin{vmatrix}
t=2\cdot e^x+1
dt=2\cdot e^x\,dx\Rightarrow dx=\frac{dt}{2\cdot e^x}
\end{vmatrix}=2\cdot\int\frac{2\cdot e^x}{t}\cdot\frac{dt}{2\cdot e^x}=2\cdot\ln|t|=2\cdot ln\left|2\cdot e^x+1\right|+c Propozycje książek
Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong
Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray
Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha
Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett
Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew
Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner
Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan
Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol
Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek
Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota
![rozwiązanie całki z funkcji [1]](https://obliczeniowo.com.pl/rownania/w_1561.gif)
![rozwiązanie całki z funkcji [3]](https://obliczeniowo.com.pl/rownania/w_1563.gif)
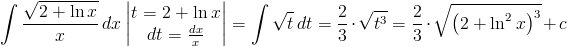
![rozwiązanie całki funkcji [7]](https://obliczeniowo.com.pl/rownania/w_1567.gif)
![rozwiązanie całki z funkcji [9]](https://obliczeniowo.com.pl/rownania/w_1569.gif)
![rozwiązanie całki z funkcji [11]](https://obliczeniowo.com.pl/rownania/w_1571.gif)
![rozwiązanie całki z funkcji [13]](https://obliczeniowo.com.pl/rownania/w_1573.gif)