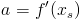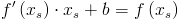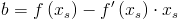Stronę tą wyświetlono już: 7974 razy

Dana jest funkcja f(x), wyznaczyć funkcję opisującą styczną do punktu x_s tejże funkcji. Prostą styczną opisuje funkcja liniowa postaci f(x)=a⋅x+b, gdzie współczynnik a jest równy tangensowi kąta α zawartego między osią x a styczną. Wartość tą stanowić będzie pochodna danej funkcji f(x).

[1]

Zapis wyrażenia w formacie TeX-a:

a=f'(x_s)

Pozostało jedynie wyznaczenie współczynnika b szukanej funkcji, a ten uzyskany zostanie poprzez przekształcenie następującej równości:

[2]

Zapis wyrażenia w formacie TeX-a:

f'\left(x_s\right)\cdot x_s+b=f\left(x_s\right)

Równość [2] wynika z faktu, iż funkcja styczna f_s(x) do funkcji f(x) musi przejść przez punkt o współrzędnych x_s, f(x_s). W wyniku przekształcenia równości [2] wyznaczona została następująca wartość parametru b:

[3]

Zapis wyrażenia w formacie TeX-a:

b=f\left(x_s\right)-f'\left(x_s\right)\cdot x_s

Ostatecznie więc ogólny wzór funkcji stycznej f_s(x) do funkcji f(x) w punkcie x_s jest następujący:

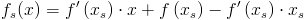[4]

Zapis wyrażenia w formacie TeX-a:

f_s(x)=f'\left(x_s\right)\cdot x+f\left(x_s\right)-f'\left(x_s\right)\cdot x_s

Przykład

Wyznaczyć wzór prostej stycznej do funkcji f(x) w punkcie x_s=3.

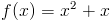
Rozwiązanie:

Podstawiając do wzoru [4] otrzymujemy następującą funkcję:

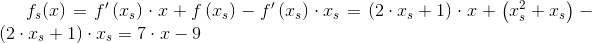
Jak widać na rysunku 1 funkcja f_s(x) jest styczna do funkcji f(x) w punkcie o współrzędnych x_s, f(x_s).