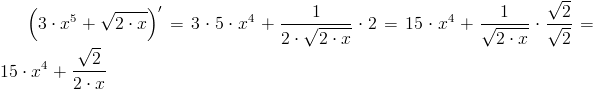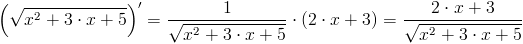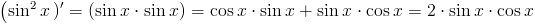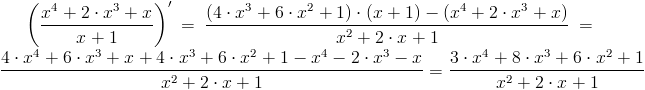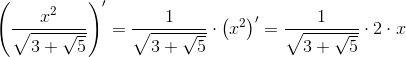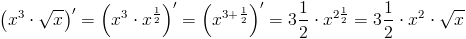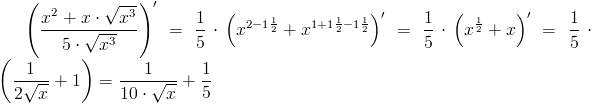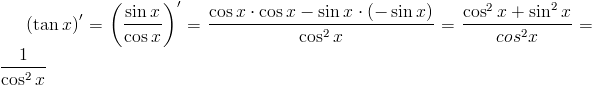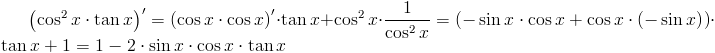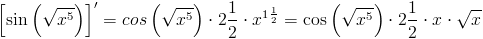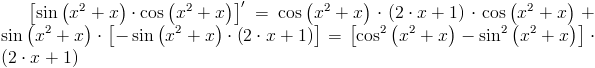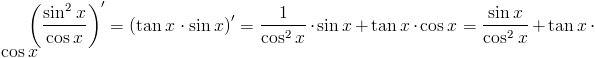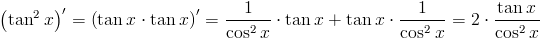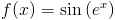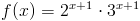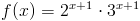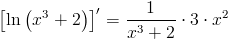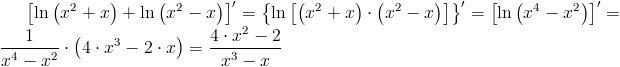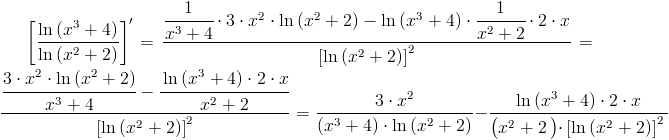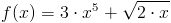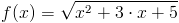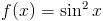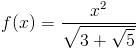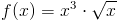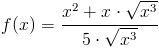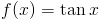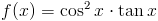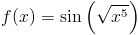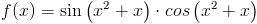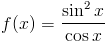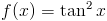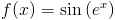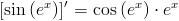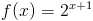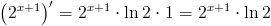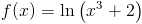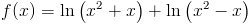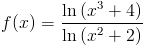Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 3195 razy

Zadanie 1 Obliczyć pochodną funkcji:

f(x)=3* x^5+sqrt(2* x)

Zapis wyrażenia w formacie TeX-a:

f(x)=3\cdot x^5+\sqrt{2\cdot x}

Rozwiązanie:

Należy zastosować twierdzenia [1], [2] oraz [6].

Obliczenie pochodnej funkcji f(x)=3* x^5+sqrt(2* x)

Zapis wyrażenia w formacie TeX-a:

\left(3\cdot x^5+\sqrt{2\cdot x}\right)'=3\cdot 5\cdot x^4+\frac{1}{2\cdot \sqrt{2\cdot x}}\cdot 2=15\cdot x^4+\frac{1}{ \sqrt{2\cdot x}}\cdot \frac{\sqrt{2}}{\sqrt{2}}=15\cdot x^4+\frac{\sqrt{2}}{2\cdot x}

Zadanie 2 Obliczyć pochodną funkcji:

f(x)=sqrt(x^2+3 * x+5)

Zapis wyrażenia w formacie TeX-a:

f(x)=\sqrt{x^2+3\cdot x+5}

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=sqrt(x^2+3*x+5)

Zapis wyrażenia w formacie TeX-a:

\left(\sqrt{x^2+3\cdot x+5}\right)'=\frac{1}{\sqrt{x^2+3\cdot x+5}}\cdot \left(2\cdot x+3\right)=\frac{2\cdot x+3}{\sqrt{x^2+3\cdot x+5}}

Zadanie 3 Obliczyć pochodną funkcji:

f(x)=sin^2x

Zapis wyrażenia w formacie TeX-a:

f(x)=sin^2x

Rozwiązanie:

Należy zastosować twierdzenie [4].

Obliczanie pochodnej funkcji f(x)=sin^2x

Zapis wyrażenia w formacie TeX-a:

\left(sin^2x\left)'=\left(sin x\cdot sin x\right)=cos x\cdot sin x+sin x\cdot cos x=2\cdot sin x\cdot cos x

Zadanie 4 Obliczyć pochodną funkcji:

f(x)=(x^4+2 * x^3+x) / (x+1)

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{x^4+2\cdot x^3+x}{x+1}

Rozwiązanie:

Należy zastosować twierdzenie [5].

Obliczenie pochodnej funkcji f(x)=(x^4+2 * x^3+x) / (x+1)

Zapis wyrażenia w formacie TeX-a:

\left(\frac{x^4+2\cdot x^3+x}{x+1}\right)'=\frac{\left(4\cdot x^3+6\cdot x^2+1\right)\cdot (x+1)-\left(x^4+2\cdot x^3+x\right)}{x^2+2\cdot x+1}=\frac{4\cdot x^4+6\cdot x^3+x+4\cdot x^3+6\cdot x^2+1-x^4-2\cdot x^3-x}{x^2+2\cdot x+1}=\frac{3\cdot x^4+8\cdot x^3 + 6\cdot x^2+1}{x^2+2\cdot x+1}

Zadanie 5 Obliczyć pochodną funkcji:

f(x)=(x^2)(sqrt(3+sqrt(5))

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{x^2}{\sqrt{3+\sqrt{5}}}

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=(x^2)(sqrt(3+sqrt(5))

Zapis wyrażenia w formacie TeX-a:

\left(\frac{x^2}{\sqrt{3+\sqrt{5}}}\right)'=\frac{1}{\sqrt{3+\sqrt{5}}}\cdot \left(x^2\right)'=\frac{1}{\sqrt{3+\sqrt{5}}}\cdot 2\cdot x

Zadanie 6 Obliczyć pochodną funkcji:

f(x)=x^3 * sqrt(x)

Zapis wyrażenia w formacie TeX-a:

f(x)=x^3\cdot \sqrt{x}

Rozwiązanie:

Obliczanie pochodnej funkcji f(x)=x^3 * sqrt(x)

Zapis wyrażenia w formacie TeX-a:

\left(x^3\cdot \sqrt{x}\right)'=\left(x^3\cdot x^{\frac{1}{2}}\right)'=\left(x^{3+\frac{1}{2}}\right)'=3\frac{1}{2}\cdot x^{2\frac{1}{2}}=3\frac{1}{2}\cdot x^2\cdot \sqrt{x}

Zadanie 7 Obliczyć pochodną funkcji:

f(x)=(x^2+x * sqrt(x^3)) / (5 * sqrt(x^3))

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{x^2+x\cdot \sqrt{x^3}}{5\cdot \sqrt{x^3}}

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=(x^2+x * sqrt(x^3)) / (5 * sqrt(x^3))

Zapis wyrażenia w formacie TeX-a:

\left(\frac{x^2+x\cdot \sqrt{x^3}}{5\cdot \sqrt{x^3}}\right)'=\frac{1}{5}\cdot \left(x^{2-1\frac{1}{2}}+x^{1+1\frac{1}{2}-1\frac{1}{2}}\right)'=\frac{1}{5}\cdot \left(x^{\frac{1}{2}}+x\right)'=\frac{1}{5}\cdot \left(\frac{1}{2\sqrt{x}}+1\right)=\frac{1}{10\cdot \sqrt{x}}+\frac{1}{5}

Zadanie 8 Obliczyć pochodną funkcji:

f(x) = tan(x)

Zapis wyrażenia w formacie TeX-a:

f(x)= \tan x

Rozwiązanie:

Rozwiązaniem pochodnej tej funkcji jest wzór [6] z strony Podstawowe wzory, jednakże tutaj ów wzór zostanie wyprowadzony.

Obliczenie pochodnej funkcji f(x) = tan(x)

Zapis wyrażenia w formacie TeX-a:

\left(tan x\right)'=\left(\frac{sin x}{cos x}\right)'=\frac{cos x\cdot cos x-sin x\cdot \left(-sin x\right)}{cos^2x}=\frac{cos^2x+sin^2 x}{cos^2x}=\frac{1}{cos^2x}
Wykorzystane zostały wzory [9], [10] z działu Matematyka: Funkcje: Funkcje trygonometryczne.

Zadanie 9 Obliczyć pochodną funkcji:

f(x)=cos^2 x * tan x

Zapis wyrażenia w formacie TeX-a:

f(x)=cos^2x\cdot\tan x

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=cos^2 x * tan x

Zapis wyrażenia w formacie TeX-a:

\left(cos^2x\cdot\tan x\right)'=\left(cos x\cdot cos x\right)'\cdot\tan x+cos^2x\cdot \frac{1}{cos^2x}=\left(-sin x\cdot cos x+cos x\cdot \left(-sin x\right)\right)\cdot\tan x+1=1-2\cdot sin x\cdot cos x\cdot\tan x

Zadanie 10 Obliczyć pochodną funkcji:

f(x)=sin(sqrt(x^5))

Zapis wyrażenia w formacie TeX-a:

f(x)=\sin\left(\sqrt{x^5}\right)

Rozwiązanie:

Obliczanie pochodnej funkcji f(x)=sin(sqrt(x^5))

Zapis wyrażenia w formacie TeX-a:

\left[sin\left(\sqrt{x^5}\right)\right]'=cos\left(\sqrt{x^5}\right)\cdot 2\frac{1}{2}\cdot x^{1\frac{1}{2}}=cos\left(\sqrt{x^5}\right)\cdot 2\frac{1}{2}\cdot x\cdot \sqrt{x}

Zadanie 11 Obliczyć pochodną funkcji:

f(x)=sin(x^2+x)* cos(x^2+x)

Zapis wyrażenia w formacie TeX-a:

f(x)=sin\left(x^2+x\right)\cdot cos\left(x^2+x\right)

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=sin(x^2+x)* cos(x^2+x)

Zapis wyrażenia w formacie TeX-a:

\left[sin\left(x^2+x\right)\cdot cos\left(x^2+x\right)\right]'=cos\left(x^2+x\right)\cdot \left(2\cdot x+1\right)\cdot cos\left(x^2+x\right)+sin\left(x^2+x\right)\cdot \left[-sin\left(x^2+x\right)\cdot \left(2\cdot x+1\right)\right]=\left[cos^2\left(x^2+x\right)-sin^2\left(x^2+x\right)\right]\cdot\left(2\cdot x+1\right)

Zadanie 12 Obliczyć pochodną funkcji:

f(x)=(sin^2 x)/(cos x)

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{sin^2 x}{cos x}

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=(sin^2 x)/(cos x)

Zapis wyrażenia w formacie TeX-a:

\left(\frac{sin^2 x}{cos x}\right)'=\left(\tan x\cdot sin x\right)'=\frac{1}{cos^2x}\cdot sin x+\tan x\cdot cos x=\frac{sin x}{cos^2x}+\tan x\cdot cos x

Zadanie 13 Obliczyć pochodną funkcji:

f(x)=tan^2x

Zapis wyrażenia w formacie TeX-a:

f(x)=\tan^2x

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=tan^2x

Zapis wyrażenia w formacie TeX-a:

\left(\tan^2x\right)'=\left(\tan x\cdot\tan x\right)'=\frac{1}{cos^2x}\cdot\tan x+\tan x\cdot\frac{1}{cos^2x}=2\cdot \frac{\tan x}{cos^2x}

Zadanie 14 Obliczyć pochodną funkcji:

f(x)=sinleft(e^x ight)

f(x)=sin(e^x)

Zapis wyrażenia w formacie TeX-a:

f(x)=sin\left(e^x\right)

Rozwiązanie:

Obliczanie pochodnej funkcji f(x)=sin(e^x)

Zapis wyrażenia w formacie TeX-a:

\left[sin\left(e^x\right)\rigt]'=cos\left(e^x\right)\cdot e^x

Zadanie 15 Obliczyć pochodną funkcji:

f(x)=2^(x+1)

Zapis wyrażenia w formacie TeX-a:

f(x)=2^{x+1}

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=2^(x+1)

Zapis wyrażenia w formacie TeX-a:

\left(2^{x+1}\right)'=2^{x+1}\cdot ln 2\cdot 1=2^{x+1}\cdot ln 2

Zadanie 16 Obliczyć pochodną funkcji:

f(x)=2^(x^2+2*x)

Zapis wyrażenia w formacie TeX-a:

f(x)=2^{x^2+2cdot x}

Rozwiązanie:

Obliczanie pochodnej funkcji f(x)=2^(x^2+2*x)

Zapis wyrażenia w formacie TeX-a:

\left(2^{x^2+2\cdot x}\right)'=2^{x^2+2\cdot x}\cdot ln 2 \cdot \left(2\cdot x+2\right)

Zadanie 17 Obliczyć pochodną funkcji:

f(x)=2^{x+1}cdot 3^{x+1}

f(x)=2^(x+1)*3^(x+1)

Zapis wyrażenia w formacie TeX-a:

f(x)=2^{x+1}cdot 3^{x+1}

Rozwiązanie:

Obliczenie pochodnej funkcji f(x)=2^(x+1)*3^(x+1)

Zapis wyrażenia w formacie TeX-a:

\left(2^{x+1}\cdot 3^{x+1}\right)'=2^{x+1}\cdot \ln 2\cdot 1\cdot 3^{x+1}+2^{x+1}\cdot 3^{x+1}\cdot ln 3\cdot 1=2^{x+1}\cdot 3^{x+1}\cdot\left(ln 2+ln 3\right)=2^{x+1}\cdot 3^{x+1}\cdot\ln 6

Zadanie 18 Obliczyć pochodną funkcji:

f(x)=ln(x^3+2)

Zapis wyrażenia w formacie TeX-a:

f(x)=ln \left(x^3+2\right)

Rozwiązanie:

Obliczanie pochodnej funkcji f(x)=ln(x^3+2)

Zapis wyrażenia w formacie TeX-a:

\left[ln \left(x^3+2\right)\right]'=\frac{1}{x^3+2}\cdot 3\cdot x^2

Zadanie 19 Obliczyć pochodną funkcji:

f(x)=ln(x^2+x)+ln(x^2-x)

Zapis wyrażenia w formacie TeX-a:

f(x)=ln \left(x^2+x\right)+ln \left(x^2-x\right)

Rozwiązanie:

Pochodna funkcji f(x)=ln(x^2+x)+ln(x^2-x)

Zapis wyrażenia w formacie TeX-a:

\left[ln \left(x^2+x\right)+ln \left(x^2-x\right)\right]'=\left{ln\left[\left(x^2+x\right)\cdot \left(x^2-x\right)\right]\right}'=\left[ln\left(x^4-x^2\right)\right]'=\frac{1}{x^4-x^2}\cdot \left(4\cdot x^3-2\cdot x\right)=\frac{4\cdot x^2-2}{x^3-x}

Zadanie 20 Obliczyć pochodną funkcji:

f(x)=(ln (x^3+4))/(ln(x^2+2))

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{ln \left(x^3+4\right)}{ln\left(x^2+2\right)}

Rozwiązanie:

Obliczanie pochodnej funkcji f(x)=(ln (x^3+4))/(ln(x^2+2))

Zapis wyrażenia w formacie TeX-a:

\left[\frac{ln \left(x^3+4\right)}{ln\left(x^2+2\right)}\right]'=\frac{\cfrac{1}{x^3+4}\cdot 3\cdot x^2 \cdot ln\left(x^2+2\right)-ln\left(x^3+4\right)\cdot \cfrac{1}{x^2+2}\cdot 2\cdot x}{\left[ln\left(x^2+2\right)\right]^2}=\frac{\cfrac{3\cdot x^2 \cdot ln\left(x^2+2\right)}{x^3+4}-\cfrac{ln\left(x^3+4\right)\cdot 2\cdot x}{x^2+2}}{\left[ln\left(x^2+2\right)\right]^2}=\frac{3\cdot x^2}{\left(x^3+4\right)\cdot ln\left(x^2+2\right)}-\frac{ln\left(x^3+4\right)\cdot 2\cdot x}{\left(x^2+2\left)\cdot \left[ln\left(x^2+2\right)\right]^2}