Wymiarowanie
Stronę tą wyświetlono już: 106556 razy
Podstawowe pojęcia
Sam rysunek techniczny nie wiele znaczy bez podania wymiarów długości liniowej bądź kątowej opisujących w jednoznaczny sposób narysowany obiekt. Często wymiarowanie umożliwia również zredukowanie potrzebnej liczby rzutów prostokątnych nawet do jednego rzutu. W końcu, wymiarowanie określa również w sposób bezpośredni lub pośredni pola tolerancji dla danego rodzaju wymiaru.
W wymiarowaniu stosuje się linie zwane wymiarowymi oraz pomocniczymi wymiarowymi. Przykład tych pierwszych jak i tych drugich można zobaczyć na poniższej ilustracji.
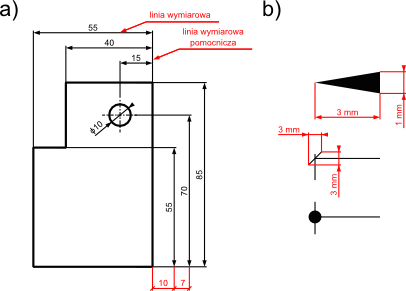
W rysunku technicznym maszynowym wszystkie wymiary podane bez jednostek są wyrażone w mm, jeżeli jakiś wymiar operuje na innych jednostkach np. calach należy na jego końcu umieścić symbol oznaczający cale, czyli ''.
Rozmieszczenie tekstu wymiarowego
Istotne jest, aby tekst wymiarowy był rozmieszczany według ścisłych zasad, dzięki czemu rysunek staje się czytelniejszy. Przykład sposobu rozmieszczania wymiarów liniowych można zobaczyć na rysunku 2. Na tym samym rysunku widać, że dla obszarów zakreskowanych zawsze wymiar podaje się poziomo na linii odniesienia (jeżeli jest to konieczne).
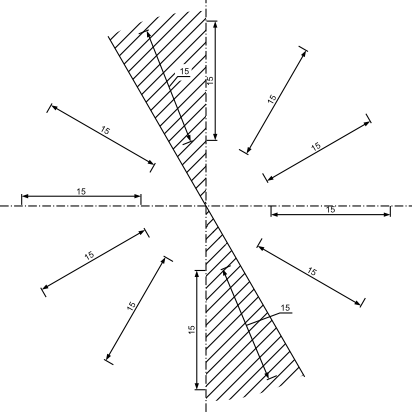
W przypadku wymiarów kątowych do dyspozycji są dwa warianty, pierwszy z liczbami pisanymi w kierunku linii wymiarowych, tak jak to widoczne jest na rysunku 3. Wyjątkiem jest tutaj oczywiście nanoszenie wymiaru kątowego w obszarze zakreskowanym, w takim przypadku wymiar pisze się poziomo z użyciem (jeżeli jest to konieczne) linii odniesienia.
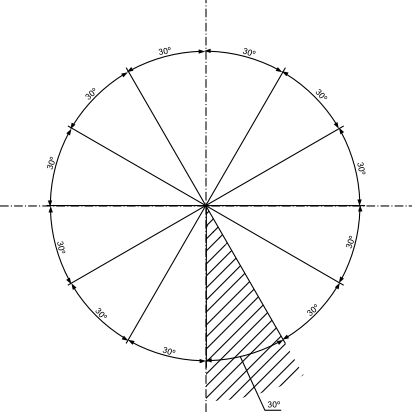
Drugi sposób widoczny jest na rysunku 4, gdzie wszystkie wymiary kątowe zapisane są poziomo, jedynie ich położenie nad lub pod linią wymiarową zależy od samego położenia mierzonej wielkości kątowej.
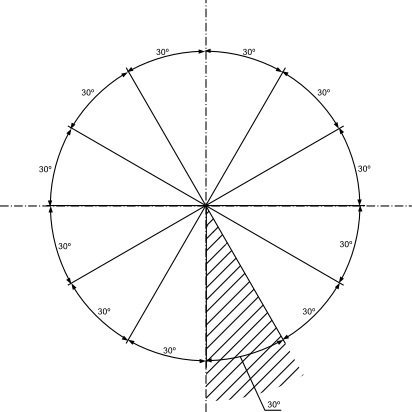
W szczególnych przypadkach, gdy brakuje miejsca można korzystać z innych zakończeń w postaci linii ukośnej lub kropki, a tekst wymiarowy umieszczać nad linią odniesienia lub na przemiennie na różnych wysokościach nad linią wymiarową tak jak pokazane zostało to na rysunku 5.
Oznaczenia używane przy wymiarowaniu
Spis oznaczeń
W celu ułatwienia wymiarowania obiektów o pewnych charakterystycznych cechach geometrycznych w rysunku technicznym stosuje się pewne symbole dające jasno do zrozumienia, z jakim typem wymiaru ma się do czynienia.
Praktyczne przykłady
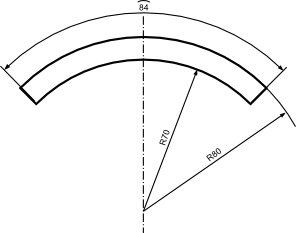
Zacznijmy od przykładu zastosowania symbolu długości łuku  oraz symbolu promienia R.
oraz symbolu promienia R.
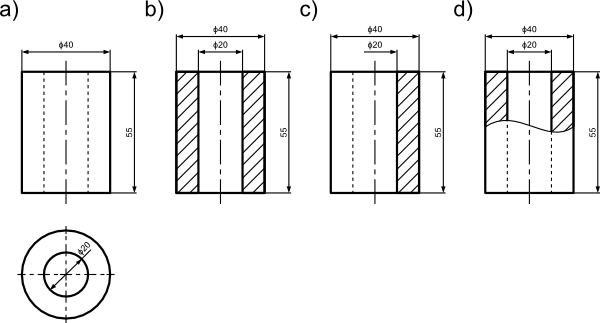
Zastosowanie symbolu średnicy ϕ często umożliwia zredukowanie liczby niezbędnych rzutów do jednego, przykładem czego jest poniższy rysunek.
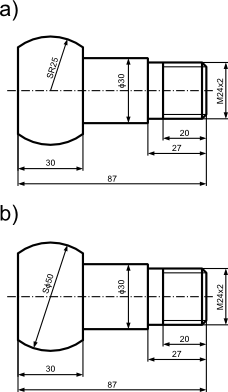
Przykład zastosowania symbolu kulistości powierzchni S.
Zastosowanie oznaczenia kwadratowej powierzchni płaskiej  umożliwia zredukowanie liczby potrzebnych rzutów do jednego. Na rysunku 9 przekreślony na czerwono został zbędny rzut w wersji b).
umożliwia zredukowanie liczby potrzebnych rzutów do jednego. Na rysunku 9 przekreślony na czerwono został zbędny rzut w wersji b).

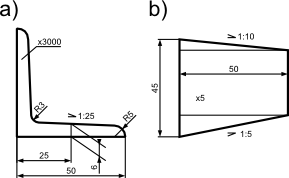
Przykłady zastosowania symbolu pochylenia powierzchni  pokazany w dwóch wariantach został na poniższym rysunku. Zastosowany został tutaj również symbol długości/grubości × obiektu.
pokazany w dwóch wariantach został na poniższym rysunku. Zastosowany został tutaj również symbol długości/grubości × obiektu.
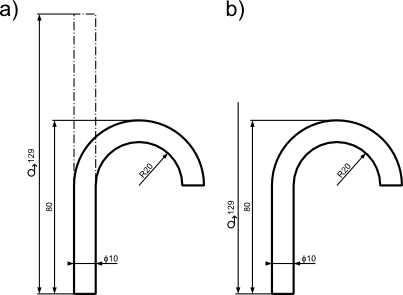
Kolejny przykład zastosowania symbolu rozwinięcia  widoczny na poniższym rysunku w dwóch wariantach.
widoczny na poniższym rysunku w dwóch wariantach.
Przykłady zastosowania symbolu n-kąta foremnego 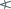 o parzystej liczbie boków.
o parzystej liczbie boków.

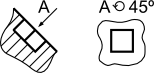
Przykłady zastosowania symbolu obrócenia widoku  .
.
Przykłady wymiarowania elementów powtarzających się
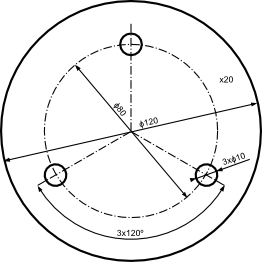
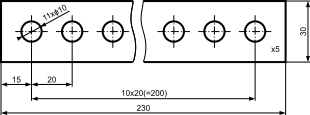
Często dochodzi do sytuacji, że na danym rysunku w jednym widoku widoczne są elementy (najczęściej otwory), które charakteryzują się takimi samymi wymiarami. W takich sytuacjach, aby nie powtarzać kilkukrotnie wymiarowania dla każdego z tych elementów stosuje się jeden wymiar z oznaczeniem liczby elementów, których on dotyczy. Przykład dla otworów można zobaczyć na rysunku 14, gdzie zastosowane zostało oznaczenie 3×ϕ10.
Istnieje również możliwość skrócenia samego rysunku z zastosowaniem jego urwania, tak jak zostało pokazane to poniżej.
Również wymiarowanie powtarzających się kształtów np. zarysu przedmiotu można uprościć stosując sposób pokazany na poniższym rysunku.

Wymiarowanie powierzchni stożkowych
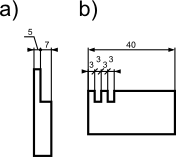
Podstawowe dwa sposoby wymiarowania krótkich powierzchni stożkowych (fazki) pokazane zostały na poniższym rysunku. Pierwsza metoda zawiera informacje o długości fazki oraz kąta w zapisie jednego wymiaru 5×45°, drugi sposób te same informacje rozbija na dwa wymiary 5 i 45°. W celu zwiększenia czytelności rysunku technicznego zaleca się stosowanie tego pierwszego sposobu dla krótkich stożków.
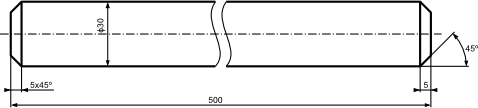
Istnieje tez bardziej uproszczony sposób oznaczenia, gdy fazka ma bardzo małe wymiary np. 0,5 [mm] co przy powiększeniu 1:1 nie jest możliwe do narysowania z zachowaniem czytelności wymiaru, wtedy rezygnuje się z rysowania fazki a jej wymiar oznacza się jak na poniższym rysunku.
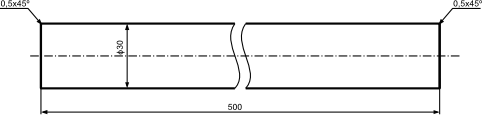
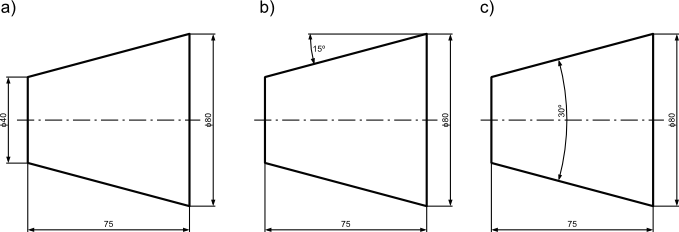
Długie stożki można wymiarować na trzy podstawowe sposoby, które pokazane zostały poniżej.
Podstawowe zasady związane z wymiarowaniem według norm PN-82/N-01614 i PN-ISO 129:1996
- Łańcuch wymiarowy nie może być zamknięty (należy stosować wymiary domyślne);
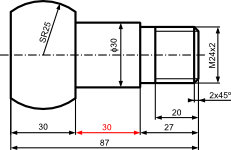 Rys. 20Przykład zamknięcia wymiarem zaznaczonym na czerwono łańcucha wymiarowego.
Rys. 20Przykład zamknięcia wymiarem zaznaczonym na czerwono łańcucha wymiarowego. - Obowiązuje zasada nie powtarzania wymiarów;
- Wysokość liczb wymiarowych powinna być taka sama (wymiary elementów wąskich należy podawać na linii odniesienia tak jak pokazane zostało to na rysunku 5);
- Linią wymiarową nie może być oś symetrii ani krawędź przedmiotu;
- Bazą wymiarowa otworu jest jego oś;
- Przy wymiarowaniu obowiązuje zasada pomijania wymiarów oczywistych;
- Należy grupować wymiary charakterystyczne elementów w jednym miejscu;
- W przypadku gdy na przekroju trzeba umieścić wymiar nie rysuje się linii kreskowania w miejscu jego wpisywania;
- Linia wymiarowa nie może być przecięta przez inną linię wymiarową lub linię pomocniczą (wyjątek stanowią tutaj linie wymiarowe okręgów współosiowych jak mna rysunku 14;
- Pomocnicze linie wymiarowe należy rysować prostopadle do wymiaru, którego dotyczą, natomiast gdy zachodzi taka konieczność rysowania ich pod ukosem obie powinny być do siebie równoległe a wymiar zaznaczony linią cienką (w ten sposób na rysunku 10 a naniesiono wymiar 6 mm;
- Linia wymiarowa powinna być ciągła, nawet wtedy gdy element, którego dotyczy pokazano jako przerwany (skrócony) czego przykładem są rysunki 17 i 18;
- Wymiary pionowe należy zawsze umieszczać z lewej strony linii wymiarowej.
