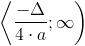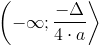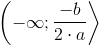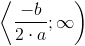Funkcje kwadratowe
Stronę tą wyświetlono już: 6010 razy
Funkcją kwadratową nazywa się funkcję następującej postaci:
gdzie:
- a, b, c - parametry liczbowe funkcji kwadratowej
Wpływ parametrów funkcji na jej przebieg
Parametr a zmienia rozpiętość paraboli, im parametr ten jest bliższy 0 tym bardziej kształt paraboli zbliża się do prostej danej wzorem g(x)=b⋅x-c. Parametr ten wpływa również na kierunek ramion, i tak gdy a<0 parabola jest skierowana ramionami w dół, gdy a>0 parabola jest skierowana ramionami ku górze. na rysunku 2 można zobaczyć parabole, których parametry a1, a2, a3 są dodatnie i spełniają następującą nierówność: a1<a2<a3.
Parametr b zmienia położenie wierzchołka funkcji kwadratowej jak na rysunku 3, gdzie parametry b1, b2, b3 spełniają następującą nierówność b1>b2>b3. Gdy b<0 wierzchołek przesuwa się w prawo, natomiast gdy b>0 wierzchołek funkcji przesuwa się w lewo.
Parametr c przesuwa w pionie wykres funkcji zmieniając tym samym położenie miejsc zerowych funkcji kwadratowej jak na rysunku 4, parametry c1, c2, c3 spełniają następującą nierówność c1<c2<c3.
Położenie wierzchołka funkcji kwadratowej
Wierzchołek funkcji kwadratowej jest zarazem minimum (gdy parametr a>0) lub maksimum (gdy parametr a<0) funkcji kwadratowej. Miejsce zerowe pochodnej funkcji kwadratowej wyznacza położenie wierzchołka tejże funkcji na osi x. Pochodna dowolnej funkcji kwadratowej jest dana następującym wzorem:
Równanie [7] jest równaniem prostej, dla której miejsce zerowe wyznaczające położenie wierzchołka funkcji kwadratowej f(x) znajduje się w punkcie danym następującym wzorem:
Do wzoru [1] za x podstawić należy wartość x0 z równania [3] w następujący sposób:
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_936.gif) | [4] |
Zapis wyrażenia w formacie TeX-a:
Ujemna wartość licznika ostatecznego wyprowadzenia wzoru [4] nazywana jest wyróżnikiem funkcji kwadratowej i oznaczana jest dużą literą alfabetu greckiego Δ. Tak więc wyznacznik ten ma następującą postać:
Ostatecznie więc współrzędne wierzchołka W funkcji kwadratowej można wyliczyć z następujących zależności:
Gdy wyróżnik Δ=0, wierzchołek funkcji kwadratowej leży na osi x (mówi się wtedy, że funkcja kwadratowa ma jedno miejsce zerowe). W przypadku gdy Δ=0 i b=0 wierzchołek funkcji kwadratowej znajduje się w początku układu współrzędnych i również ma jedno miejsce zerowe. Gdy Δ>0, funkcja kwadratowa ma dwa rzeczywiste miejsca zerowe a jej wierzchołek leży na osi y, gdy współczynnik b=0. Jeżeli wyróżnik Δ<0 to funkcja kwadratowa posiada dwa miejsca zerowe leżące w zbiorze liczb zespolonych, a jej wierzchołek również leży na osi y, gdy b=0.
Miejsca zerowe funkcji kwadratowej
Podstawą do wyznaczenia wzoru na miejsca zerowe funkcji kwadratowej jest określenie położenia jej wierzchołka W, ponieważ odległość od niego do miejsc zerowych x1, x2 jest taka sama (rysunek 11). Wystarczy teraz wyznaczyć odległość |Wx-x1|, wykorzystując w tym celu znaną odległość Wy.
Oznaczając umownie przez Δx szukaną odległość |Wx-x1|, można zapisać następną równość:
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_939.gif) | [7] |
Zapis wyrażenia w formacie TeX-a:
Powyższą równość otrzymuje się poprzez pominięcie we wzorze f(x)=a⋅x2+b⋅x+c czynnika b⋅x+c, podstawienie za f(x) współrzędnej Wy wierzchołka funkcji kwadratowej oraz za x zmienną Δx. Teraz pozostało jedynie do współrzędnej Wx dodać i odjąć uzyskaną wartość Δx otrzymując wzory na współrzędne miejsc zerowych x1, x2.
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_940.gif) | [8] |
Zapis wyrażenia w formacie TeX-a:
Gdy wyróżnik Δ=0, wzór [8] przyjmuje następującą uproszczoną postać:
Gdy wyróżnik Δ<0 funkcja ma dwa miejsca zerowe w zbiorze liczb zespolonych.
Kanoniczna postać równania kwadratowego
Postać kanoniczna funkcji kwadratowej zawiera wyrażenia, będące współrzędnymi wierzchołka tej funkcji i ma następującą postać:
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_942.gif) | [10] |
Zapis wyrażenia w formacie TeX-a:
Postać iloczynowa równania kwadratowego
W skład tejże postaci równania kwadratowego wchodzą jej pierwiastki (wartości miejsc zerowych).
Dla Δ=0:
Dla Δ≠0:
Pierwiastki x1, x2 równania kwadratowego dla wyróżnika Δ<0 są liczbami urojonymi.
Postać ogólna równania kwadratowego - patrz równanie [1]
Własności funkcji kwadratowej
Dziedzina funkcji Df∈(-∞;∞)
Przeciwdziedzina funkcji należy do zbioru:
gdy a>0;
gdy a<0
Dla a>0 funkcja malejąca, dla a<0 rosnąca w przedziale:
natomiast dla a>0 funkcja rosnąca, dla a<0 malejąca w przedziale:
Wartości funkcji kwadratowej dla wyróżnika Δ<0 przyjmują znak zgodny z znakiem wartości parametru a funkcji.
Gdy Δ=0, funkcja przybiera wartości zgodne ze znakiem wartości parametru a z wyjątkiem punktu wierzchołka tejże funkcji.
Gdy Δ>0, funkcja przyjmuje wartości dodatnie gdy a>0, i ujemne gdy a<0 w przedziałach (-∞; x1);∪(x2;∞), natomiast wartości dodatnie dla a>0 oraz ujemna dla a<0 w przedziale (x1;x2). W punktach x1, x2 funkcja przyjmuje wartości zerowe.<
Wierzchołek W funkcji kwadratowej stanowi jej maksimum globalne gdy a<0, natomiast minimum globalne gdy a>0.

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_933.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_934.gif)
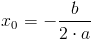
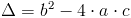
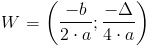
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_941.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_943.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_944.gif)