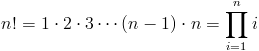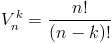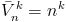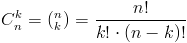Silnia

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 7014 razy

Operator silni, którego symbolem jest wykrzyknik dany jest następującym wzorem:

wzór opisujący działanie operatora silni w matematyce

Zapis wyrażenia w formacie TeX-a:

n!=1\cdot 2\cdot 3 \cdots (n-1)\cdot n=\prod_{i=1}^{n}{i}

Oczywiście liczba n musi należeć do zbioru liczb naturalnych N, a argumenty dla kolejno po sobie następujących wartości liczby n rosną bardzo szybko:<

1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800

Najbardziej znane zastosowanie operator silni znajduje w podstawowych wzorach wyznaczających prawdopodobieństwo zdarzeń. I tak na przykład permutacja bez powtórzeń n-elementowego zbioru obliczana jest według następującej zależności:

[2]

Zapis wyrażenia w formacie TeX-a:

P_n=n!

Permutacja bez powtórzeń zbioru n-elementowego określa liczbę wszystkich możliwych ułożeń elementów danego zbioru, jeżeli więc dany będzie zbiór 10 różnych elementów, to liczba możliwych ułożeń owych elementów wynosić będzie 10!=3628800.

Permutacja z powtórzeniami n-elementowego zbioru składającego się z k różnych elementów dana jest następującym wzorem:

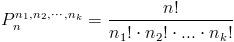[3]

Zapis wyrażenia w formacie TeX-a:

P_{n}^{n_1, n_2, \cdots, n_k}=\frac{n!}{n_1!\cdot n_2!\cdot ...\cdot n_k!}

i określa ona, liczbę możliwych ułożeń zbioru, w którym co najmniej jeden z k różnych elementów zbioru powtarza się więcej niż jeden raz, a n₁, n₂,...,n_k są liczbami powtórzeń danego elementu w danym zbiorze. Suma owych powtórzeń jest równa n.

Również wzór na k-elementową wariację bez powtórzeń n-elementowego zbioru wykorzystuje silnię w następujący perfidny sposób:

[4]

Zapis wyrażenia w formacie TeX-a:

V_{n}^{k}=\frac{n!}{(n-k)!}

W wzorze [4] musi być spełniony następujący warunek k≤n, przy czym gdy k=n równie dobrze można zastosować wzór [2], ponieważ 0!=1.<

Wzór na wariację k-elentową bez powtórzeń zbioru n-elementowego nie zawiera co prawda operatora silni, jednakże przy okazji warto go tutaj mimo wszystko przedstawić:

[5]

Zapis wyrażenia w formacie TeX-a:

\bar{V}_{n}^{k}=n^k

Kombinacja k-elementowa bez powtórzeń zbioru n-elementowego można obliczyć według wzoru następującego:

[6]

Zapis wyrażenia w formacie TeX-a:

C_n^k=\left( _k^n\right)=\frac{n!}{k!\cdot(n-k)!}

W wzorze [6] musi zostać zachowany następujący warunek k≤n.

Kombinacja k-elementowa z powtórzeniami zbioru n-elementowego z kolei może zostać obliczona za pomocą wzoru następującego:

[7]

Zapis wyrażenia w formacie TeX-a:

\bar{C}_n^k=\left( _{n-1}^{n+k-1}\right)=\left( _{k}^{n+k-1}\right)=\frac{(n+k-1)!}{k!(n-1)!}

Wymienione tutaj wzory umożliwiają obliczenie prawdopodobieństwa zdarzeń, związanych z skończonymi zbiorami rozwiązań, np odwrotność permutacji bez powtórzeń określa prawdopodobieństwo ułożenia wszystkich elementów danego zbioru według jednej wybranej kolejności.

Operator silni wykorzystywany jest w szeregu Taylora, wyznaczającym wartości funkcji trygonometrycznych w następujący sposób:

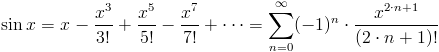[8]

Zapis wyrażenia w formacie TeX-a:

sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots =\sum_{n=0}^\infty (-1)^n\cdot\frac{x^{2\cdot n+1}}{(2\cdot n+1)!}

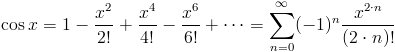[9]

Zapis wyrażenia w formacie TeX-a:

\cos x &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots =\sum_{n=0}^\infty(-1)^n\frac{x^{2\cdot n}}{(2\cdot n)!}

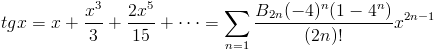[10]

Zapis wyrażenia w formacie TeX-a:

tg x = x + \frac{x^3}{3} + \frac{2 x^5}{15} + \cdots =\sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}

gdzie:

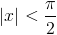
$|x|<frac{pi}{2}$
B_n - liczby Bernoulliego

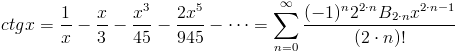[11]

Zapis wyrażenia w formacie TeX-a:

ctg x= \frac {1} {x} - \frac {x}{3} - \frac {x^3} {45} - \frac {2 x^5} {945} - \cdots =\sum_{n=0}^\infty \frac{(-1)^n 2^{2\cdot n} B_{2\cdot n} x^{2\cdot n-1}}{(2\cdot n)!}

gdzie: